题目内容
1.已知x>0,y>0,x+y+3=xy,且不等式(x+y)2-a(x+y)+1≥0恒成立.则实数a的取值范围是a≤$\frac{37}{6}$.分析 由基本不等式和题意可得x+y的范围,变形恒成立的式子由函数的单调性可得.
解答 解:∵x>0,y>0,x+y+3=xy,
∴由基本不等式可得x+y+3=xy≤($\frac{x+y}{2}$)2,
解关于x+y的不等式可得x+y≥6,
∵不等式(x+y)2-a(x+y)+1≥0恒成立,
∴a≤(x+y)+$\frac{1}{x+y}$恒成立,
由函数单调性可得当x+y=6时(x+y)+$\frac{1}{x+y}$取最小值$\frac{37}{6}$,
∴a≤$\frac{37}{6}$,
故答案为:a≤$\frac{37}{6}$.
点评 本题考查基本不等式求最值,涉及函数的单调性,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.△ABC中,角A,B,C的对边分别为a,b,c,a:b:c=2:3:4,则$\frac{sinA-2sinB}{sin2C}$等于( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
6.已知复数z的实部为2,虚部为1,则(2-i)z=( )
| A. | 4+i | B. | 4-i | C. | 5 | D. | 4 |

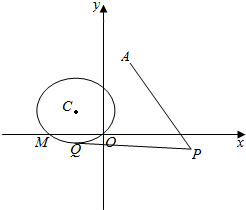 圆C过点M(-2,0)及原点,且圆心C在直线x+y=0上.
圆C过点M(-2,0)及原点,且圆心C在直线x+y=0上.