题目内容
19.函数y=$\frac{\sqrt{tanx}}{sinx}$的定义域.分析 根据函数成立的条件即可求函数的定义域.
解答 解:要使函数有意义,则$\left\{\begin{array}{l}{tanx≥0}\\{sinx≠0}\end{array}\right.$,
即$\left\{\begin{array}{l}{kπ≤x<kπ+\frac{π}{2},k∈Z}\\{x≠kπ}\end{array}\right.$,即kπ<x<kπ+$\frac{π}{2}$,k∈Z,
即函数的定义域为(kπ,kπ+$\frac{π}{2}$),k∈Z.
点评 本题主要考查函数定义域的求解,根据三角函数的图象和性质是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.对条件语句的描述正确的是( )
| A. | ESLE后面的语句不可以是条件语句 | |
| B. | 两个条件语句可以共用一个END IF语句 | |
| C. | 条件语句可以没有ELSE后的语句 | |
| D. | 条件语句中IF-THEN语句和ELSE后的语句必须同时存在 |
14.已知椭圆的两个焦点分别为F1、F2,其中F1与抛物线x2=8y的焦点重合,过F1且不与x轴平行的直线与椭圆交于A、B两点,若△ABF2为等腰直角三角形,则e2=( )
| A. | 7-4$\sqrt{3}$ | B. | 5-2$\sqrt{6}$ | C. | 9-6$\sqrt{2}$ | D. | 8-2$\sqrt{15}$ |
11.△ABC中,角A,B,C的对边分别为a,b,c,a:b:c=2:3:4,则$\frac{sinA-2sinB}{sin2C}$等于( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
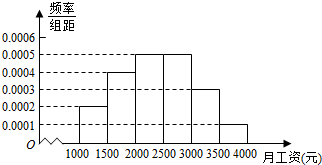 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图如图所示.(每个分组包括左端点,不包括右端点,如第一组表示[1000,1500).
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图如图所示.(每个分组包括左端点,不包括右端点,如第一组表示[1000,1500).