题目内容
正四棱台的体对角线是5cm,高是3cm,求它的两条相对侧棱所确定的截面的面积.
考点:平面的基本性质及推论,棱台的结构特征
专题:计算题,空间位置关系与距离
分析:如图所示,过D1作D1E⊥BD于E,则D1E=3cm,利用四边形BDD1B1为等腰梯形,即可求出两条相对侧棱所确定的截面的面积.
解答:
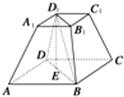 解:如图所示,过D1作D1E⊥BD于E,则D1E=3cm.
解:如图所示,过D1作D1E⊥BD于E,则D1E=3cm.
∵对角线BD1=5cm,
∴在Rt△BD1E中,BE=4cm.
设棱台上、下底面的边长分别为a、b,
则BD=
b,B1D1=
a.
又∵四边形BDD1B1为等腰梯形,
且DE=
(b-a)=BD-BE=
b-4,
∴
(a+b)=8.
∴SBDD1B1=
(B1D1+BD)•D1E=
×
(a+b)×3=12(cm2).
 解:如图所示,过D1作D1E⊥BD于E,则D1E=3cm.
解:如图所示,过D1作D1E⊥BD于E,则D1E=3cm.∵对角线BD1=5cm,
∴在Rt△BD1E中,BE=4cm.
设棱台上、下底面的边长分别为a、b,
则BD=
| 2 |
| 2 |
又∵四边形BDD1B1为等腰梯形,
且DE=
| ||
| 2 |
| 2 |
∴
| 2 |
∴SBDD1B1=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
点评:本题考查棱台的结构特征,考查两条相对侧棱所确定的截面的面积,考查学生的计算能力,比较基础.

练习册系列答案
相关题目




 如图所示,在空间四边形ABCD中,AB=BC,CD=DA,E、F、G分别为CD、DA和AC的中点.求证:平面BEF⊥平面BGD.
如图所示,在空间四边形ABCD中,AB=BC,CD=DA,E、F、G分别为CD、DA和AC的中点.求证:平面BEF⊥平面BGD. 如图所示.△ABC中,AB>AC,作∠FBC=∠ECB=
如图所示.△ABC中,AB>AC,作∠FBC=∠ECB=