题目内容
13.在直角坐标系中,曲线C的参数方程为,$\left\{\begin{array}{l}{x=\sqrt{5}cosφ}\\{y=\sqrt{15}sinφ}\end{array}\right.$(ϕ为参数),直线l的参数方程为$\left\{\begin{array}{l}{x=-\frac{1}{2}t}\\{y=\sqrt{3}+\frac{\sqrt{3}}{2}t}\end{array}\right.$(t为参数).以原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为$(\sqrt{3},\frac{π}{2})$.(Ⅰ)求点P的直角坐标,并求曲线C的普通方程;
(Ⅱ)设直线l与曲线C的两个交点为A,B,求|PA|+|PB|的值.
分析 (I)消参数即可得到普通方程,根据极坐标的几何意义即可得出P的直角坐标;
(II)将l的参数方程代入曲线C的普通方程得出A,B对应的参数,利用参数得几何意义得出|PA|+|PB|.
解答 解:(Ⅰ)$x=\sqrt{3}cos\frac{π}{2}=0$,y=$\sqrt{3}$sin$\frac{π}{2}$=$\sqrt{3}$,∴P的直角坐标为$P(0,\sqrt{3})$;
由$\left\{\begin{array}{l}{x=\sqrt{5}cosφ}\\{y=\sqrt{15}sinφ}\end{array}\right.$得cosφ=$\frac{x}{\sqrt{5}}$,sinφ=$\frac{y}{\sqrt{15}}$.∴曲线C的普通方程为$\frac{x^2}{5}+\frac{y^2}{15}=1$.
(Ⅱ)将$\left\{\begin{array}{l}{x=-\frac{1}{2}t}\\{y=\sqrt{3}+\frac{\sqrt{3}}{2}t}\end{array}\right.$代入$\frac{x^2}{5}+\frac{y^2}{15}=1$ 得t2+2t-8=0,
设A,B对应的参数分别为t1,t2,则t1+t2=-2,t1t2=-8,
∵P点在直线l上,
∴|PA|+|PB|=|t1|+|t2|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$=6.
点评 本题考查了参数方程与普通方程的互化,参数得几何意义,属于基础题.

练习册系列答案
相关题目
4.已知两条不同的直线a,b,三个不同的平面α,β,γ,下列说法正确的是( )
| A. | 若a∥α,b⊥a,则b∥α | B. | 若a∥α,a∥β,则α∥β | C. | 若α⊥β,a⊥α,则a∥β | D. | 若α⊥γ,β∥γ,则α⊥β |
8.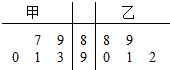 甲、乙两名学生五次数学测验成绩(百分制)如图所示.
甲、乙两名学生五次数学测验成绩(百分制)如图所示.
①甲同学成绩的中位数大于乙同学成绩的中位数;
②甲同学的平均分与乙同学的平均分相等;
③甲同学成绩的方差大于乙同学成绩的方差.
以上说法正确的是( )
 甲、乙两名学生五次数学测验成绩(百分制)如图所示.
甲、乙两名学生五次数学测验成绩(百分制)如图所示.①甲同学成绩的中位数大于乙同学成绩的中位数;
②甲同学的平均分与乙同学的平均分相等;
③甲同学成绩的方差大于乙同学成绩的方差.
以上说法正确的是( )
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
5.已知集合A={-1,0,1,2},B={x|x<2},则A∩B=( )
| A. | {-1,0,1} | B. | {-1,0,2} | C. | {-1,0} | D. | {0,1} |
2.若函数f(x),g(x)分别是定义在R上的奇函数和偶函数,且满足f(x)+g(x)=ex,则下列结论正确的是( )
| A. | f(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$且0<f(1)<g(2) | B. | f(x)=$\frac{{e}^{x}+{e}^{-x}}{2}$且0<f(1)<g(2) | ||
| C. | f(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$且g(2)<f(1)<0 | D. | f(x)=$\frac{{e}^{x}+{e}^{-x}}{2}$且g(2)<f(1)<0 |