题目内容
四棱锥S-ABCD的底面是菱形，SD⊥平面ABCD，点E是SD的中点．
（Ⅰ）求证：SB∥平面EAC；
（Ⅱ）求证：平面SAC⊥平面SBD．
（Ⅰ）求证：SB∥平面EAC；
（Ⅱ）求证：平面SAC⊥平面SBD．
考点：平面与平面垂直的判定,直线与平面平行的判定
专题：空间位置关系与距离
分析：（Ⅰ）连结AC，BD，交于点O，连结OE，由三角形中位线得OE∥SB，由此能证明SB∥平面EAC．
（Ⅱ）由菱形性质得AC⊥BD，由线面垂直得SD⊥AC，由此能证明平面SAC⊥平面SBD．
（Ⅱ）由菱形性质得AC⊥BD，由线面垂直得SD⊥AC，由此能证明平面SAC⊥平面SBD．
解答：
证明：（Ⅰ）连结AC，BD，交于点O，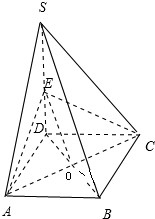
连结OE，
∵ABCD是菱形，∴O是AC中点，
又E是SD中点，∴OE∥SB，
∵OE?平面AEC，SB?平面AEC，
∴SB∥平面EAC．
（Ⅱ）∵ABCD是菱形，∴AC⊥BD，
∵SD⊥平面ABCD，AC?平面ABCD，
∴SD⊥AC，
∵SD∩BD=D，
∴AC⊥平面SBD，
∵AC?平面SAC，∴平面SAC⊥平面SBD．
连结OE，∵ABCD是菱形，∴O是AC中点，
又E是SD中点，∴OE∥SB，
∵OE?平面AEC，SB?平面AEC，
∴SB∥平面EAC．
（Ⅱ）∵ABCD是菱形，∴AC⊥BD，
∵SD⊥平面ABCD，AC?平面ABCD，
∴SD⊥AC，
∵SD∩BD=D，
∴AC⊥平面SBD，
∵AC?平面SAC，∴平面SAC⊥平面SBD．
点评：本题考查直线与平面平行的证明，考查平面与平面垂直的证明，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
如图，已知AB⊥面ACD，DE⊥面ACD，△ACD为等边三角形，AD=DE=2AB，F为CD的中点，
如图，棱柱ABCD-A1B1C1D1的所有棱长都等于2，∠ABC=60°，平面AA1C1C⊥平面ABCD，∠A1AC=60°．
如图，在三棱锥P-ABC中，除棱PC外，其余棱均等长，M为棱AB的中点，O为线段MC上靠近点M的三等分点．