题目内容
 如图,已知AB⊥面ACD,DE⊥面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点,
如图,已知AB⊥面ACD,DE⊥面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点,(1)求证:AF∥面BCE;
(2)求二面角A-CE-D的正切值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间角
分析:(1)根据线面平行的判定定理即可证明AF∥面BCE;
(2)根据二面角的定义,先求出二面角的平面角即可得到结论.
(2)根据二面角的定义,先求出二面角的平面角即可得到结论.
解答:
证明:(1)取CE的中点P,连结FP,BP,
∵F为CD的中点,
∴FP∥DE且FP=
DE,
又AB∥DE,且AB=
DE,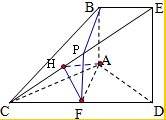
∴AB∥FP,且AB=FP,
∴ABPF为平行四边形,∴AF∥BP,
∵AF?平面BCE,BP?平面BCE,
∴AF∥面BCE;
(2)过F作FH⊥CE,连AH,设AB=1
则CE⊥面AFH,得CE⊥AH,
∵AF⊥CD,
∴∠AHF就是二面角A-CE-D平面角,
则AF=
AD=
,FH=
,
Rt△AFH中,tan∠AHF=
=
,
即二面角A-CE-D的正切值
.
∵F为CD的中点,
∴FP∥DE且FP=
| 1 |
| 2 |
又AB∥DE,且AB=
| 1 |
| 2 |

∴AB∥FP,且AB=FP,
∴ABPF为平行四边形,∴AF∥BP,
∵AF?平面BCE,BP?平面BCE,
∴AF∥面BCE;
(2)过F作FH⊥CE,连AH,设AB=1
则CE⊥面AFH,得CE⊥AH,
∵AF⊥CD,
∴∠AHF就是二面角A-CE-D平面角,
则AF=
| ||
| 2 |
| 3 |
| ||
| 2 |
Rt△AFH中,tan∠AHF=
| AF |
| HF |
| 6 |
即二面角A-CE-D的正切值
| 6 |
点评:本题主要考查空间直线和平面平行的判定,以及空间二面角的计算,要求熟练掌握线面平行的判定定理,以及二面角的求解方法.

练习册系列答案
相关题目
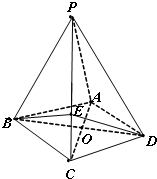 如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD.PA=AB=2,∠BAD=120°,E是PC上的一点,且BE与平面PAB所成角的正弦值为
如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD.PA=AB=2,∠BAD=120°,E是PC上的一点,且BE与平面PAB所成角的正弦值为