题目内容
9.已知sin2x-$\sqrt{3}$cos2x=2cos(2x-θ)(-π<θ<π),则θ=$\frac{5π}{6}$.分析 由条件利用两角和差的余弦公式,诱导公式可得cos(2x-$\frac{5π}{6}$)=cos(2x-θ),由此求得θ的值.
解答 解:∵sin2x-$\sqrt{3}$cos2x=2cos(2x-θ)(-π<θ<π),∴sin(2x-$\frac{π}{3}$)=cos(2x-θ),
即 cos(2x-$\frac{5π}{6}$)=cos(2x-θ),∴θ=$\frac{5π}{6}$,
故答案为:$\frac{5π}{6}$.
点评 本题主要考查两角和差的余弦公式,诱导公式的应用,属于基础题.

练习册系列答案
相关题目
19.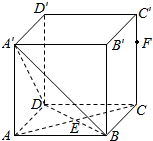 如图,正方体ABCD-A′B′C′D′中,$\overrightarrow{BD}=2\overrightarrow{BE}$.设点F在线段CC'上,直线EF与平面A'BD所成的角为α,则sinα的取值范围是( )
如图,正方体ABCD-A′B′C′D′中,$\overrightarrow{BD}=2\overrightarrow{BE}$.设点F在线段CC'上,直线EF与平面A'BD所成的角为α,则sinα的取值范围是( )
 如图,正方体ABCD-A′B′C′D′中,$\overrightarrow{BD}=2\overrightarrow{BE}$.设点F在线段CC'上,直线EF与平面A'BD所成的角为α,则sinα的取值范围是( )
如图,正方体ABCD-A′B′C′D′中,$\overrightarrow{BD}=2\overrightarrow{BE}$.设点F在线段CC'上,直线EF与平面A'BD所成的角为α,则sinα的取值范围是( )| A. | $[\frac{{\sqrt{3}}}{3},1]$ | B. | $[\frac{{2\sqrt{2}}}{3},1]$ | C. | $[\frac{{\sqrt{6}}}{3},\frac{{2\sqrt{2}}}{3}]$ | D. | $[\frac{{\sqrt{6}}}{3},1]$ |