题目内容
2. 定义在实数R上的函数y=f(x)是偶函数,当x≥0时,f(x)=-4x2+8x-3.
定义在实数R上的函数y=f(x)是偶函数,当x≥0时,f(x)=-4x2+8x-3.(Ⅰ)求f(x)在R上的表达式;
(Ⅱ)在给出的坐标系中作出y=f(x)的图象,并写出f(x)最大值和f(x)在R上的单调区间.
分析 (Ⅰ)x<0时,-x>0,代入已知x≥0时,f(x)=-4x2+8x-3,可得f(-x)=-4x2-8x-3,根据偶函数的性质可求得f(x)=-4x2-8x-3;
(Ⅱ)根据解析式可作出y=f(x)的图象,根据二次函数的单调性分别求解两段函数的单调区间即可.
解答 解:(Ⅰ)设x<0,则-x>0,f(-x)=-4(-x)2+8(-x)-3=-4x2-8x-3,(2分)
∵f(x)是偶函数,∴f(-x)=f(x),
∴x<0时,f(x)=-4x2-8x-3,
∴f(x)=$\left\{\begin{array}{l}{-4{x}^{2}+8x-3,x≥0}\\{-4{x}^{2}-8x-3,x<0}\end{array}\right.$;
(Ⅱ)如图所示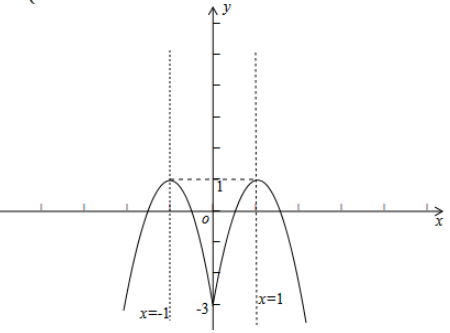
由图可知y=f(x)有最大值f(1)=f(-1)=1
函数y=f(x)的单调递增区间是(-∞,-1]和[0,1]
单调递减区间是[-1,0]和[1,+∞)
点评 本题主要考查了利用偶函数的对称性求解函数的解析式,函数单调性的判断与证明,函数的单调区间的求解,(Ⅱ)中对每段函数求解单调区间时要注意函数的定义域.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
12.已知tan(π-α)=-$\frac{2}{3}$,且α∈(-π,-$\frac{π}{2}}$),则$\frac{{cos({-α})+3sin({π+α})}}{{cos({π-α})+9sinα}}$的值为( )
| A. | $-\frac{1}{5}$ | B. | $-\frac{3}{7}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{7}$ |
13.设{an}为等比数列,{bn}为等差数列,且b1=0,cn=an+bn,若数列{cn}是1,1,2,…,则{cn}的前10项和为( )
| A. | 979 | B. | 557 | C. | 467 | D. | 978 |
10.有下列命题:
①若xy=0,则|x|+|y|=0;
②若a>b,则a+c>b+c;
③矩形的对角线互相垂直,
其中真命题共有( )
①若xy=0,则|x|+|y|=0;
②若a>b,则a+c>b+c;
③矩形的对角线互相垂直,
其中真命题共有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
7.若2sinα+cosα=-$\sqrt{5}$,则tanα=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
11.已知角α的顶点与原点O重合,始边与x轴的非负半轴重合,P(m,-2m)(m≠0)是角α终边上的一点.则tan(α+$\frac{π}{4}$)的值为( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | $-\frac{1}{3}$ | D. | -3 |