题目内容
7．若2sinα+cosα=-$\sqrt{5}$，则tanα=（ ）| A． | $\frac{1}{2}$ | B． | 2 | C． | -$\frac{1}{2}$ | D． | -2 |
分析 利用辅角公式求得sin（α+φ）的值，利用正弦函数的性质求得α+φ的值，再利用同角三角函数的基本关系和诱导公式求得tanα．
解答 解：由2sinα+cosα=-$\sqrt{5}$，得$\sqrt{5}$sin（α+φ）=-$\sqrt{5}$（其中tanφ=$\frac{1}{2}$），
即有sin（α+φ）=-1，
所以α+φ=2kπ-$\frac{π}{2}$，α=2kπ-$\frac{π}{2}$-φ（k∈Z），
所以tanα=tan（-$\frac{π}{2}$-φ）=$\frac{1}{tanφ}$=2．
故选：B．
点评 本题主要考查了同角三角函数的基本关系的应用和诱导公式的化简求值，是基础题目．
练习册系列答案
相关题目
17．在△ABC中，已知2asinA+csinC=bsinB，则∠B为（ ）
| A． | 钝角 | B． | 锐角 | C． | 直角 | D． | 不能 |
定义在实数R上的函数y=f（x）是偶函数，当x≥0时，f（x）=-4x2+8x-3．
12．与y=x为同一函数的是（ ）
| A． | y=（$\sqrt{x}$）2 | B． | y=$\frac{{x}^{2}}{x}$ | C． | y=$\left\{\begin{array}{l}{x，（x＞0）}\\{-x，（x＜0）}\end{array}\right.$ | D． | y=$\root{3}{{x}^{3}}$ |
19．
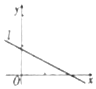设（x1，y1），（x2，y2），…，（xn，yn）是变量x和y的n个样本点，直线l是由这些样本点通过最小二乘法得到的线性回归直线（如图），则下列结论正确的是（ ）
设（x1，y1），（x2，y2），…，（xn，yn）是变量x和y的n个样本点，直线l是由这些样本点通过最小二乘法得到的线性回归直线（如图），则下列结论正确的是（ ）| A． | x和y成正相关 | |
| B． | 若直线l方程为$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$，则$\widehat{b}$＞0 | |
| C． | 最小二乘法是使尽量多的样本点落在直线上的方法 | |
| D． | 直线l过点$（\overline x，\overline y）$ |
16．已知集合A={1，2，3}，B={-2，-1，0，1，2}，则A∩B=（ ）
| A． | {1，2，3} | B． | {-2，-1，0，1，2} | C． | {1，2} | D． | {-2，-1} |