题目内容
11．已知角α的顶点与原点O重合，始边与x轴的非负半轴重合，P（m，-2m）（m≠0）是角α终边上的一点．则tan（α+$\frac{π}{4}$）的值为（ ）| A． | 3 | B． | $\frac{1}{3}$ | C． | $-\frac{1}{3}$ | D． | -3 |
分析 由条件利用任意角的三角函数的定义求得tanα，再利用两角和的正切公式，特殊角的三角函数值即可计算得解．
解答 解：根据P（m，-2m）（m≠0）是角α终边上的一点，
可得：tanα=$\frac{-2m}{m}$=-2，
可得：tan（α+$\frac{π}{4}$）=$\frac{1+tanα}{1-tanα}$=$\frac{1-2}{1+2}$=-$\frac{1}{3}$．
故选：C．
点评 本题主要考查任意角的三角函数的定义，特殊角的三角函数值、两角和的正切公式的应用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
定义在实数R上的函数y=f（x）是偶函数，当x≥0时，f（x）=-4x2+8x-3．
19．
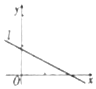设（x1，y1），（x2，y2），…，（xn，yn）是变量x和y的n个样本点，直线l是由这些样本点通过最小二乘法得到的线性回归直线（如图），则下列结论正确的是（ ）
设（x1，y1），（x2，y2），…，（xn，yn）是变量x和y的n个样本点，直线l是由这些样本点通过最小二乘法得到的线性回归直线（如图），则下列结论正确的是（ ）| A． | x和y成正相关 | |
| B． | 若直线l方程为$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$，则$\widehat{b}$＞0 | |
| C． | 最小二乘法是使尽量多的样本点落在直线上的方法 | |
| D． | 直线l过点$（\overline x，\overline y）$ |
6．已知a、b都为集合{-2，0，1，3，4}中的元素，则函数f（x）=（a2-2）x+b为增函数的概率是（ ）
| A． | $\frac{2}{5}$ | B． | $\frac{3}{5}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{10}$ |
16．已知集合A={1，2，3}，B={-2，-1，0，1，2}，则A∩B=（ ）
| A． | {1，2，3} | B． | {-2，-1，0，1，2} | C． | {1，2} | D． | {-2，-1} |