题目内容
9.已知椭圆$\frac{{x}^{2}}{49}$+$\frac{{y}^{2}}{24}$=1的左、右焦点分别为F1、F2,点A在椭圆上,且|AF2|=6,则△AF1F2的面积是24.分析 根据椭圆方程求得离心率及右准线方程,根据椭圆的第二定义,求得A点横坐标,代入椭圆方程求得纵坐标,根据三角形面积公式△AF1F2的面积是$\frac{1}{2}$•2c•|yA,即可求得△AF1F2的面积.
解答 解:椭圆$\frac{{x}^{2}}{49}$+$\frac{{y}^{2}}{24}$=1,a=7,b=2$\sqrt{6}$,
c=$\sqrt{49-24}$=5,
由离心率e=$\frac{c}{a}$=$\frac{5}{7}$,
右准线方程为x=$\frac{{a}^{2}}{c}$=$\frac{49}{5}$,
|AF2|=ed=e($\frac{{a}^{2}}{c}$-xA)=a-exA=6,
即为7-$\frac{5}{7}$xA=6,可得xA=$\frac{7}{5}$,
yA=±$\sqrt{24(1-\frac{1}{25})^{2}}$=±$\frac{24}{5}$,
则△AF1F2的面积是$\frac{1}{2}$•2c•|yA|
=5•$\frac{24}{5}$=24.
故答案为:24.
点评 本题考查椭圆的简单性质,椭圆的第二定义的应用,三角形的面积公式,考查分析问题及解决问题的能力,属于中档题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
4.在一次随机试验中,彼此互斥的事件A,B,C,D的概率分别是0.2,0.1,0.3,0.4,则下列说法正确的是( )
| A. | A+B与C是互斥事件,也是对立事件 | |
| B. | B+C与D是互斥事件,也是对立事件 | |
| C. | A+C与B+D是互斥事件,但不是对立事件 | |
| D. | A与B+C+D是互斥事件,也是对立事件 |
1.曲线y=$\frac{lnx-2x}{x}$在点(1,f(1))处的切线方程为( )
| A. | y=x-3 | B. | y=-x+1 | C. | y=2x-2 | D. | y=-2x+2 |
19.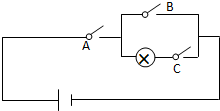 如图所示电路,有A、B、C三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且相互独立,则灯泡亮的概率( )
如图所示电路,有A、B、C三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且相互独立,则灯泡亮的概率( )
 如图所示电路,有A、B、C三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且相互独立,则灯泡亮的概率( )
如图所示电路,有A、B、C三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且相互独立,则灯泡亮的概率( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{16}$ |
 在直三棱柱中,AA1=AB=BC=2,AC=1,D是AC中点.
在直三棱柱中,AA1=AB=BC=2,AC=1,D是AC中点.