题目内容
4．若f（x）是周期为2的奇函数，当0≤x≤1时，f（x）=2x（1-x），则f（2017.5）=$-\frac{1}{2}$．分析 根据已知中函数的周期性和奇偶性，可得f（2017.5）=f（-0.5）=-f（0.5），进而得到答案．
解答 解：∵当0≤x≤1时，f（x）=2x（1-x），
∴f（0.5）=$\frac{1}{2}$，
由f（x）是奇函数，
可得：f（-0.5）=f（-0.5）=-$\frac{1}{2}$，
由f（x）是周期为2的周期函数，
可得：f（2017.5）=f（-0.5）=$-\frac{1}{2}$，
故答案为：$-\frac{1}{2}$
点评 本题考查的知识点是抽象函数及其应用，函数的周期性，函数的奇偶性，函数求值，难度中档．
练习册系列答案
相关题目
12．
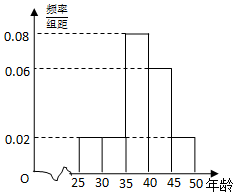某企业员工500人参加“学雷锋”志愿活动，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50]，得到的频率分布直方图如图：
（1）如表是年龄的频数分布表，求a，b的值；
（2）根据频率分布直方图估计志愿者年龄的平均数和中位数；
（3）现在要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，则年龄在第1，2，3组的分别抽取多少人？
（4）在（3）的前提下，从这6人中随机抽取2人参加社区宣传交流活动，求至少有1人年龄在第3组的概率．
某企业员工500人参加“学雷锋”志愿活动，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50]，得到的频率分布直方图如图：（1）如表是年龄的频数分布表，求a，b的值；
| 区间 | [25，30） | [30，35） | [35，40） | [40，45） | [45，50] |
| 人数 | 50 | 50 | a | 150 | b |
（3）现在要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，则年龄在第1，2，3组的分别抽取多少人？
（4）在（3）的前提下，从这6人中随机抽取2人参加社区宣传交流活动，求至少有1人年龄在第3组的概率．
19．若$θ∈（0，\frac{π}{4}）$，化简$\sqrt{1-2sin（3π-θ）sin（\frac{π}{2}+θ）}$=（ ）
| A． | sinθ-cosθ | B． | sinθ+cosθ | C． | cosθ+sinθ | D． | cosθ-sinθ |
13．在区间（1，7）上任取一个数，这个数在区间（5，8）上的概率为（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
14．在等差数列{an}中，已知a4+a8=16，则a2+a6+a10=（ ）
| A． | 12 | B． | 16 | C． | 20 | D． | 24 |