题目内容

20．在区间（0，+∞）上不是增函数的是（　　）
A．y=3x-2B．y=3x2-1C．y=2x2+3xD．y=$\frac{2}{x}$-1

分析 判断函数在区间（0，+∞）上是不是增函数，即可得到结果．

解答 解：y=3x-2在区间（0，+∞）上是增函数，
y=3x2-1对称轴是x=0，在区间（0，+∞）上是增函数，
y=2x2+3x对称轴为：x=-$\frac{3}{2}$，在区间（0，+∞）上是增函数，
y=$\frac{2}{x}$-1，在区间（0，+∞）上是减函数．
故选：D．

点评 本题考查函数的单调性的判断与应用，是基础题．

练习册系列答案
相关题目
10．若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞b＞0）的渐近线和圆x2+y2-6y+8=0相切，则该双曲线的离心率等于（　　）
A．$\sqrt{2}$B．2C．3D．$\sqrt{3}$
11．x2+（y+2）2=3的圆心坐标、半径分别为（　　）
A．（0，2）；3B．（0，-2）；3C．$（{0，2}）；\sqrt{3}$D．$（{0，-2}）；\sqrt{3}$
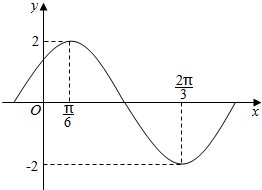8．设-$\sqrt{2}$≤a≤$\sqrt{2}$，b≠0，a，b∈R，则（a-b）2+（$\sqrt{2-{a}^{2}}$-$\frac{9}{b}$）2的最小值为8．
15．函数$f（x）=Asin（ωx+φ）\;（A＞0，ω＞0，|φ|＜\frac{π}{2}）$部分图象如图所示．
（Ⅰ）求f（x）的最小正周期及解析式；
（Ⅱ）求函数f（x）的单调递减区间；
（Ⅲ）设g（x）=f（x）-2cos2x，求函数g（x）在区间$[0，\frac{π}{2}]$上的值域．
5．从集合A到集合B的映射f：x→x2+1，若A={-2，-1，0，1，2}，则B中至少有3个元素．
12．计算题
（1）求值：${27^{\frac{2}{3}}}-{（{\root{3}{-125}}）^2}-{2^{{{log}_2}3}}×{log_2}\frac{1}{8}+{log_2}3×{log_3}4$
（2）求不等式的解集：①33-x＜2；②${log_5}（{x-1}）＜\frac{1}{2}$．
9．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点F（1，0），且经过点P（$\frac{1}{2}$，$\frac{3\sqrt{5}}{4}$）
（1）求椭圆C的方程；
（2）若直线l与椭圆C相切，过F作FQ⊥l，垂足为Q，求证：|OQ|为定值（其中O为坐标原点）．
10．如图，空间四边形PABC中，PA，PB，PC两两垂直，∠PBC=60°，求BC与平面PAB所成的角．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网