题目内容
6. 如图,在直四棱柱(侧棱与底面垂直的四棱柱)ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC,给出以下结论:
如图,在直四棱柱(侧棱与底面垂直的四棱柱)ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC,给出以下结论:①异面直线A1B1与CD1所成的角为45°;
②D1C⊥AC1;
③在棱DC上存在一点E,使D1E∥平面A1BD,这个点为DC的中点;
④在棱AA1上不存在点F,使三棱锥F-BCD的体积为直 四棱柱体积的$\frac{1}{5}$.
其中正确的有①②③.
分析 直接利用已知条件推出异面直线所成的角判断①的正误;通过直线与平面的直线关系判断②的正误;通过直线与平面的平行判断③的正误;几何体的体积判断④的正误即可
解答 解:①由题意可知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC,所以△DD1C1是等腰直角三角形,A1B1∥C1D1,异面直线A1B1与CD1所成的角为45°,所以①正确.
②由题意可知,AD⊥平面DD1C1C,四边形DD1C1C是正方形,所以D1C⊥DC1,
可得D1C⊥AC1;所以②正确;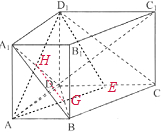
③在棱DC上存在一点E,使D1E∥平面A1BD,这个点为DC的中点,因为:
DC=DD1=2AD=2AB,如图HG∥D1E且HG=$\frac{1}{2}$D1E,所以E为中点,所以③正确.
④设AB=1,则棱柱的体积为:$\frac{1}{2}$ (1+2)×1×1=$\frac{3}{2}$,
当F在A1时,A1-BCD的体积为:$\frac{1}{3}$×$\frac{1}{2}$×1×2×1=$\frac{1}{3}$,
显然体积比为$\frac{2}{9}$>$\frac{1}{5}$,
所以在棱AA1上存在点F,使三棱锥F-BCD的体积为直四棱柱体积的$\frac{1}{5}$,所以④不正确.
正确结果有①②③.
故答案为:①②③.
点评 本题考查棱柱的结构特征,几何体的体积的求法,直线与平面的位置关系的判断,考查空间想象能力计算能力

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
1.已知球的表面积为64π,则它的体积为( )
| A. | 16π | B. | $\frac{256}{3}$π | C. | 36π | D. | $\frac{100}{3}$π |
11.设a=lg$\frac{2}{3}$,b=lg$\frac{2}{5}$,c=lg$\frac{3}{2}$,则( )
| A. | a>c>b | B. | b>c>a | C. | c>b>a | D. | c>a>b |