题目内容
16．从5名男生和4名女生中选出4人参加辩论比赛，如果4人中男生和女生各两人，则不同的选法种数为60．分析 利用组合知识，结合乘法原理，可得结论
解答 解：∵从5名男生和4名女生中选出4人参加学校辩论赛，
∴4人中男生和女生各选2人，共有${C}_{5}^{2}{C}_{4}^{2}$=60种方法，
故答案为60．
点评 本题考查组合知识，考查学生的计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
6．在四面体ABCD中，AB⊥AD，AB=AD=BC=CD=1，且平面ABD⊥平面BCD，M为AB中点，则CM与平面ABD所成角的正弦值为（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{6}}}{3}$ |
7．
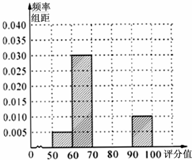某单位进行了主题为“你幸福吗”的幸福指数问卷调查，得到每个调查对象的幸福指数评分值（百分制）．现从收到的调查表中随机抽取20份进行统计，得到如图所示的频率分布表和频率分布直方图．
（Ⅰ）请完成题目中的频率分布表，并补全题目中的频率分布直方图；
（Ⅱ）该单位将随机邀请被问卷调查的部分员工参加“幸福教育”的座谈会．在抽样统计的这20人中，已知幸福指数评分值在区间（80，100]的5人中有2人被邀请参加座谈，求其中幸福指数评分值在区间（80，90]的仅有1人被邀请的概率．
某单位进行了主题为“你幸福吗”的幸福指数问卷调查，得到每个调查对象的幸福指数评分值（百分制）．现从收到的调查表中随机抽取20份进行统计，得到如图所示的频率分布表和频率分布直方图．（Ⅰ）请完成题目中的频率分布表，并补全题目中的频率分布直方图；
（Ⅱ）该单位将随机邀请被问卷调查的部分员工参加“幸福教育”的座谈会．在抽样统计的这20人中，已知幸福指数评分值在区间（80，100]的5人中有2人被邀请参加座谈，求其中幸福指数评分值在区间（80，90]的仅有1人被邀请的概率．
| 幸福指数评分值 | 频数 | 频率 |
| [50，60] | ||
| （60，70] | ||
| （70，80] | ||
| （80，90] | 3 | |
| （90，100] | ||
| 合 计 | 20 | 1 |
如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，且AD∥BC，∠ABC=90°，PA⊥面ABCD，若PA=AB=BC=$\frac{1}{2}$AD．
1．某产品的广告费用x（万元）与销售额y（百万元）的统计数据如表：
根据上表可得回归方程$\widehat{y}$=$\widehat{b}x+\widehat{a}$中的$\widehat{a}$为2.3，据此模型预报广告费用为12万元时销售额为8.3百万元．
| 广告费用x（万元） | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 销售额y（百万元） | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
8．抛掷两枚质地均匀的骰子，向上的点数之和为7的概率是（ ）
| A． | $\frac{1}{9}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{18}$ | D． | $\frac{1}{12}$ |