题目内容
2.已知复数z=$\frac{10{i}^{2016}}{(3+i)^{2}}$,则在复平面内,复数z所对应的点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 利用复数单位的幂运算,然后利用复数的乘法的运算法则化简求解即可.
解答 解:z=$\frac{10{i}^{2016}}{(3+i)^{2}}$=$\frac{10}{8+6i}$=$\frac{5}{4+3i}$$\frac{5(4-3i)}{(4+3i)(4-3i)}$=$\frac{4}{5}$-$\frac{3i}{5}$,
对应点的坐标($\frac{4}{5}$,-$\frac{3}{5}$),
故选:D.
点评 本题考查复数的代数形式的混合运算,复数的几何意义,考查计算能力.

练习册系列答案
相关题目
12.已知P,Q,R是圆x2+y2-2x-8=0上不同三点,它们到直线l:x+$\sqrt{3}$y+7=0的距离分别为x1,x2,x3,若x1,x2,x3成等差数列,则公差的最大值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.已知实数x,y满足$\left\{\begin{array}{l}{2x+y≥4}\\{4x-y≤8}\\{x-y≥-1}\end{array}\right.$,则x2+y2-2x的取值范围是( )
| A. | [-$\frac{1}{5}$,19] | B. | [-$\frac{1}{5}$,+∞) | C. | [3,19] | D. | [-$\frac{1}{5}$,3] |
3.如图,正方体ABCD-A1B1C1D1中,棱长为1,点P在体对角线上,PB=$\frac{1}{3}$PB′,则P点坐标为( )
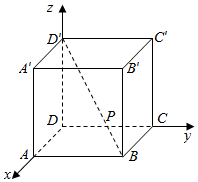

| A. | ($\frac{1}{3}$$,\frac{1}{3}$,$\frac{1}{3}$) | B. | ($\frac{2}{3}$,$\frac{2}{3}$,$\frac{2}{3}$) | C. | ($\frac{5}{6}$,$\frac{5}{6}$,$\frac{1}{6}$) | D. | ($\frac{2}{3}$,$\frac{2}{3}$,$\frac{1}{3}$) |