题目内容
19.若x,y满足约束条件$\left\{\begin{array}{l}{x+y>1}\\{x-y≥-1}\\{2x-y≤2}\end{array}\right.$,且目标函数z=ax+2y仅在点(1,0)处取得最小值,则a的取值范围是( )| A. | (-1,2) | B. | (-4,2) | C. | (-4,0) | D. | (-4,2) |
分析 作出不等式组对应的平面区域,利用目标函数的意义,确定目标函数的斜率关系即可得到结论.
解答 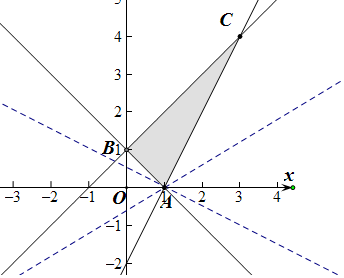 解:画出区域图,可知当a=0时,z=2y,即y=$\frac{1}{2}$z,符合题意;
解:画出区域图,可知当a=0时,z=2y,即y=$\frac{1}{2}$z,符合题意;
当a>0时,y=-$\frac{a}{2}$x+$\frac{1}{2}$z,斜率-$\frac{a}{2}$>-1,即0<a<2时符合题意;
当a<0时,y=-$\frac{a}{2}$x+$\frac{1}{2}$z,斜率-$\frac{a}{2}$<2,即-4<a<0时符合题意;
综上,a∈(-4,2),
故选:B.
点评 本题主要考查线性规划的应用,利用数形结合是解决本题的关键,要注意对a进行分类讨论.

练习册系列答案
相关题目
10.已知正三棱锥P-ABC的外接球的球心O满足$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=0,则二面角A-PB-C的正弦值为( )
| A. | $\frac{1}{6}$ | B. | $\frac{\sqrt{2}}{8}$ | C. | $\frac{2\sqrt{6}}{5}$ | D. | $\frac{\sqrt{6}}{3}$ |
7. 某三棱锥的三视图如图所示,其中三个视图都是直角三角形,则该三棱锥外接球的体积为( )
某三棱锥的三视图如图所示,其中三个视图都是直角三角形,则该三棱锥外接球的体积为( )
 某三棱锥的三视图如图所示,其中三个视图都是直角三角形,则该三棱锥外接球的体积为( )
某三棱锥的三视图如图所示,其中三个视图都是直角三角形,则该三棱锥外接球的体积为( )| A. | 2π | B. | $\sqrt{6}π$ | C. | 6π | D. | $4\sqrt{3}π$ |
14.为了调查中学生课外阅读古典文学名著的情况,某校学生会从男生中随机抽取了50人,从女生中随机抽取了60人参加古典文学名著知识竞赛,统计数据如表所示,经计算K2≈8.831,则测试成绩是否优秀与性别有关的把握为( )
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| 优秀 | 非优秀 | 总计 | |
| 男生 | 35 | 15 | 50 |
| 女生 | 25 | 35 | 60 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.500 | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 0.455 | 2.706 | 3.841 | 6.635 | 10.828 |
| A. | 90% | B. | 95% | C. | 99% | D. | 99.9% |
4.某几何体三视图如图所示,则该几何体的表面积为( )
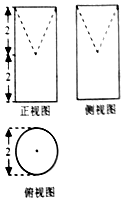

| A. | (9+$\sqrt{5}$)π | B. | (9+2$\sqrt{5}$)π | C. | (10+$\sqrt{5}$)π | D. | (10+2$\sqrt{5}$)π |
9.已知的取值如表所示:
如果y与x线性相关,且线性回归方程$y=bx+\frac{13}{2}$,则$\stackrel{∧}{b}$=( )
| x | 2 | 3 | 4 |
| y | 6 | 4 | 5 |
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{4}$ | D. | $-\frac{5}{6}$ |