题目内容
11.已知函f(x)=sin(2x-$\frac{π}{6}$)-cos2x.(Ⅰ)求函数f(x)的最小正周期、最大值及取得最大值时x的集合;
(Ⅱ)设△ABC内角A、B、C的对边分别为a、b、c,若$f(\frac{B}{2})=-\frac{{\sqrt{3}}}{2}$,b=1,$c=\sqrt{3}$,且a>b,求角B和角C.
分析 (I)根据两角差的正弦公式、特殊角的三角函数值化简解析式,由三角函数的周期公式函数f(x)的最小正周期,由正弦函数的最值求出最大值及取得最大值时x的集合;
(II)由(Ⅰ)化简$f(\frac{B}{2})=-\frac{\sqrt{3}}{2}$,由B的范围和特殊角的三角函数值求出B,由条件和正弦定理列出方程求出sinC,由C的范围和特殊角的三角函数值求出C,并结合条件验证边角关系.
解答 解:(Ⅰ)由题意得,f(x)=sin2xcos$\frac{π}{6}$-cos2xsin$\frac{π}{6}$-cos2x…(1分)
=$\frac{{\sqrt{3}}}{2}sin2x-\frac{3}{2}cos2x=\sqrt{3}sin(2x-\frac{π}{3})$…(2分)
∴函数f(x)的最小正周期为$T=\frac{2π}{2}=π$…(3分)
当$2x-\frac{π}{3}=2kπ+\frac{π}{2}$,即$x=kπ+\frac{5}{12}π,k∈Z$时,
f(x)取最大值为$\sqrt{3}$,…(4分)
这时x的集合为$\{x|x=kπ+\frac{5}{12}π,k∈Z\}$…(5分)
(Ⅱ)由(I)知,$f(\frac{B}{2})=\sqrt{3}sin(B-\frac{π}{3})=-\frac{{\sqrt{3}}}{2}$,
∴$sin(B-\frac{π}{3})=-\frac{1}{2}$,…(6分)
∵0<B<π,∴$-\frac{π}{3}<B-\frac{π}{3}<\frac{2π}{3}$…(7分)
∴$B-\frac{π}{3}=-\frac{π}{6},即B=\frac{π}{6}$,…(8分)
$又∵b=1,c=\sqrt{3}$,
∴由正弦定理得$\frac{b}{sinB}=\frac{c}{sinC}$,则$sinC=\frac{csinB}{b}=\frac{{\sqrt{3}}}{2}$,…(9分)
∵C为三角形的内角,∴$C=\frac{π}{3}或\frac{2π}{3}$…(10分)
$当C=\frac{π}{3}时,A=\frac{π}{2}$;…(11分)
$当C=\frac{2π}{3}时,A=\frac{π}{6}$,
由a>b得A>B,则$A=\frac{π}{6}$舍去,
∴$B=\frac{π}{6},C=\frac{π}{3}$…(12分)
点评 此题考查了两角和与差的正弦、余弦函数公式,正弦定理,正弦函数的最值,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键,注意内角的范围和边角关系.

| A. | {x|-1<x<1} | B. | {x|x≥-2} | C. | {x|-2≤x<1} | D. | {x|-1<x≤2} |
| A. | (-1,2) | B. | (-4,2) | C. | (-4,0) | D. | (-4,2) |
| A. | .{1,8} | B. | .{1,3,7,8} | C. | .{1,5,7,8} | D. | {1,3,5,7,8} |
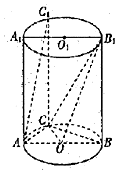 如图,在圆柱OO1中,矩形ABB1A1是过OO1的截面CC1是圆柱OO1的母线,AB=2,AA1=3,∠CAB=$\frac{π}{3}$.
如图,在圆柱OO1中,矩形ABB1A1是过OO1的截面CC1是圆柱OO1的母线,AB=2,AA1=3,∠CAB=$\frac{π}{3}$.