题目内容
8．cos（-$\frac{17}{4}$π）+sin（-$\frac{17}{4}$π）的值是0．分析 由条件利用诱导公式进行化简所给的式子，可得结果．
解答 解：cos（-$\frac{17}{4}$π）+sin（-$\frac{17}{4}$π）=cos（-$\frac{π}{4}$）+sin（-$\frac{π}{4}$）=cos$\frac{π}{4}$-sin$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{2}$=0，
故答案为：0．
点评 本题主要考查利用诱导公式进行化简求值，属于基础题．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
19．若x，y满足约束条件$\left\{\begin{array}{l}{x+y＞1}\\{x-y≥-1}\\{2x-y≤2}\end{array}\right.$，且目标函数z=ax+2y仅在点（1，0）处取得最小值，则a的取值范围是（ ）
| A． | （-1，2） | B． | （-4，2） | C． | （-4，0） | D． | （-4，2） |
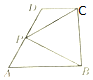如图，在直角梯形ABCD中，AB∥CD，AB⊥BC，AB=2，CD=1，BC=a（a＞0），P为线段AD（含端点）上一个动点，设$\overrightarrow{AP}=x\overrightarrow{AD}，\overrightarrow{PB}•\overrightarrow{PC}=y$，对于函数y=f（x），给出以下三个结论：①当a=2时，函数f（x）的值域为[1，4]；②对于任意的a＞0，均有f（1）=1；③对于任意的a＞0，函数f（x）的最大值均为4．其中所有正确的结论序号为②③．
17．设双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的左、右焦点分别为F1，F2，过F2的直线与双曲线的右支交于两点A，B，若|AF1|：|AB|=3：4，且F2是AB的一个四等分点，则双曲线C的离心率是（ ）
| A． | $\frac{{\sqrt{5}}}{2}$ | B． | $\frac{{\sqrt{10}}}{2}$ | C． | $\frac{5}{2}$ | D． | 5 |