题目内容
方程x2+y2+x+y-m=0表示一个圆,则m的取值范围是( )
A、m>-
| ||
B、m<-
| ||
C、m≤-
| ||
D、m≥-
|
考点:二元二次方程表示圆的条件
专题:计算题,直线与圆
分析:由二元二次方程表示圆的条件得到m的不等式,解不等式即可得到结果.
解答:
解:∵方程x2+y2+x+y-m=0表示一个圆,
∴1+1+4m>0,
∴m>-
故选:A.
∴1+1+4m>0,
∴m>-
| 1 |
| 2 |
故选:A.
点评:本题考查二元二次方程表示圆的条件,属基础知识的考查,本题解题的关键是看清楚所表示的二元二次方程的各个系数之间的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知圆C:(x-2)2+y2=1和两点A(0,a)与B(0,-a)(a>0),若圆C上存在一点P使得PA⊥PB,则a的取值范围是( )
| A、(0,3] |
| B、(0,1] |
| C、[1,3] |
| D、[3,+∞) |
某几何体的三视图的形状和尺寸如图所示,则其体积是( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
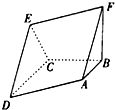 如图空间几何体ABCDEF中,四边形ADEF为平行四边形,FB⊥平面ABCD,AB∥CD,AB⊥BC,AB=BC=
如图空间几何体ABCDEF中,四边形ADEF为平行四边形,FB⊥平面ABCD,AB∥CD,AB⊥BC,AB=BC=