题目内容
已知函数f(x)=ex-m-x,其中m为常数.
(1)若对任意x∈R有f(x)≥0恒成立,求m的取值范围;
(2)当m>1时,判断f(x)在[0,2m]上零点的个数,并说明理由.
解 (1)依题意,可知f(x)在R上连续,
且f′(x)=ex-m-1,令f′(x)=0,得x=m,
故当x∈(-∞,m)时,ex-m<1,f′(x)<0,f(x)单调递减;
当x∈(m,+∞)时,ex-m>1,f′(x)>0,f(x)单调递增.
故当x=m时,f(m)为极小值也是最小值.
令f(m)=1-m≥0,得m≤1.
即对任意x∈R,f(x)≥0恒成立时,m的取值范围是(-∞,1].
(2)当m>1时,f(m)=1-m<0.
∵f(0)=e-m>0,f(0)·f(m)<0,且f(x)在(0,m)上单调递减,
∴f(x)在(0,m)上有一个零点.
又f(2m)=em-2m,令g(m)=em-2m,
∵当m>1时,g′(m)=em-2>0,
∴g(m)在(1,+∞)上单调递增.
∴g(m)>g(1)=e-2>0,即f(2m)>0.
∴f(m)·f(2m)<0,∴f(x)在(m,2m)上有一个零点.故f(x)在[0,2m]上有两个零点.

下表是函数值y随自变量x变化的一组数据,它最可能的函数模型是( )
| x | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 15 | 17 | 19 | 21 | 23 | 25 | 27 |
A.一次函数模型 B.幂函数模型
C.指数函数模型 D.对数函数模型
已知函数f(x)的定义域是[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.
| x | -1 | 0 | 2 | 4 | 5 |
| f(x) | 1 | 2 | 1.5 | 2 | 1 |

下列关于函数f(x)的命题:
①函数f(x)的值域为[1,2];
②函数f(x)在[0,2]上是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)-a最多有4个零点.
其中正确命题的序号是________.
 B.
B.
 D.
D.
 f(x)·g(x)dx=0,则称f(x),g(x)为区间[-1,1]上的一组正交函数.给出三组函数:
f(x)·g(x)dx=0,则称f(x),g(x)为区间[-1,1]上的一组正交函数.给出三组函数: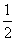 x,g(x)=cos
x,g(x)=cos 的符号;
的符号;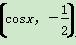 ,b=(
,b=(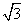 sinx,cos2x),x∈R,设函数f(x)=a·b.
sinx,cos2x),x∈R,设函数f(x)=a·b. 上的最大值和最小值.
上的最大值和最小值.