题目内容
10.已知tna2α=-$\frac{4}{3}$,α是第一象限角,则tanα等于( )| A. | 1 | B. | 3 | C. | 4 | D. | 2 |
分析 由已知可得tanα>0,利用二倍角的正切函数公式整理可得2tan2α-3tanα+2=0,从而解得tanα的值.
解答 解:∵α是第一象限角,tanα>0,且tan2α=$\frac{2tanα}{1-ta{n}^{2}α}$=-$\frac{4}{3}$,
∴整理可得:2tan2α-3tanα+2=0,
∴解得:tanα=2或-$\frac{1}{2}$(舍去).
故选:D.
点评 本题主要考查了二倍角的正切函数公式在三角函数求值中的应用,考查了计算能力,属于基础题.

练习册系列答案
相关题目
1.已知$\overrightarrow{a}$=2,$\overrightarrow{b}$=1,$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=5,则$\overrightarrow{a}$,$\overrightarrow{b}$夹角的余弦值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2\sqrt{3}}{5}$ | D. | $\frac{\sqrt{2}}{2}$ |
5.函数y=3cosx是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
 函数f(x)=sin(ωx+φ)(ω>0,φ∈[0,2π])的部分图象如图所示,则f(2013)=-1.
函数f(x)=sin(ωx+φ)(ω>0,φ∈[0,2π])的部分图象如图所示,则f(2013)=-1. 的顶点都在半径为
的顶点都在半径为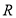 的球
的球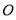 的球面上,且
的球面上,且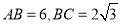 ,棱锥
,棱锥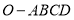 的体积为
的体积为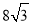 ,则
,则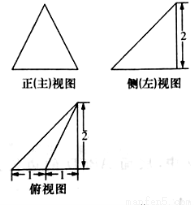
 B.
B.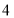 C.
C.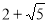 D.
D.
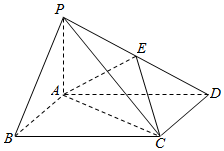 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.