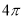题目内容
18. 函数f(x)=sin(ωx+φ)(ω>0,φ∈[0,2π])的部分图象如图所示,则f(2013)=-1.
函数f(x)=sin(ωx+φ)(ω>0,φ∈[0,2π])的部分图象如图所示,则f(2013)=-1.
分析 由周期求出ω,由五点法作图求出φ的值,可得函数f(x)的解析式,从而求得f(2013)的值.
解答 解:结合函数f(x)=sin(ωx+φ)(ω>0,φ∈[0,2π])的部分图象,
可得$\frac{1}{4}•\frac{2π}{ω}$=3-1,ω=$\frac{π}{4}$,
再根据五点法作图可得$\frac{π}{4}$•1+φ=$\frac{π}{2}$,求得φ=$\frac{π}{4}$,故f(x)=sin($\frac{π}{4}$x+$\frac{π}{4}$),
f(2013)=sin($\frac{2013π}{4}$+$\frac{π}{4}$)=sin(503π+$\frac{π}{2}$)=-1,
故答案为:-1.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由五点法作图求出φ的值,可得函数f(x)的解析式,从而求得f(2013)的值.

练习册系列答案
相关题目
12.直线y-4=-$\sqrt{3}$(x+3)的倾斜角和所过的定点分别是( )
| A. | -60°,(-3,4) | B. | 120°,(-3,4) | C. | 150°,(-3,4) | D. | 120°,(3,-4) |
9.函数f(x)=Acos(ωx+φ)(A>0,ω>0)在x=2015处取得最小值,则( )
| A. | f(x-2015)一定是奇函数 | B. | f(x-2015)一定是偶函数 | ||
| C. | f(x+2015)一定是奇函数 | D. | f(x+2015)一定是偶函数 |
6.下列叙述正确的是( )
| A. | 数列1,3,5,7与7,5,3,1是相同的数列 | |
| B. | 数列0,1,2,3,…可以表示为{n} | |
| C. | 数列0,1,0,1,…是常数列 | |
| D. | 数列{$\frac{n}{n+1}$}是递增数列 |
10.已知tna2α=-$\frac{4}{3}$,α是第一象限角,则tanα等于( )
| A. | 1 | B. | 3 | C. | 4 | D. | 2 |
 截球
截球 的球面所得圆的半径为
的球面所得圆的半径为 ,球心
,球心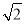 ,则球
,则球 B.
B. C.
C.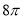 D.
D.