题目内容
13.在平面直角坐标系中,以原点为极点,x轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.已知曲线C的极坐标方程为ρ=2cosθ,直线l的参数方程为$\left\{\begin{array}{l}x=-1+tcosα\\ y=tsinα\end{array}\right.$(t为参数,α为直线的倾斜角).(I)写出直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)若直线l与曲线C有唯一的公共点,求角α的大小.
分析 (Ⅰ)通过当$α=\frac{π}{2}$时,当$α≠\frac{π}{2}$时,分别求出直线l的普通方程.由ρ=2cosθ,得ρ2=2ρcosθ,然后求解曲线C的直角坐标方程.
(Ⅱ)把x=-1+tcosα,y=tsinα代入x2+y2=2x,利用△=0,求解直线l倾斜角α.
解答 解:(Ⅰ)当$α=\frac{π}{2}$时,直线l的普通方程为x=-1;
当$α≠\frac{π}{2}$时,直线l的普通方程为y=(tanα)(x+1).…(2分)
由ρ=2cosθ,得ρ2=2ρcosθ,
所以x2+y2=2x,即为曲线C的直角坐标方程.…(4分)
(Ⅱ)把x=-1+tcosα,y=tsinα代入x2+y2=2x,整理得t2-4tcosα+3=0.当α=$\frac{π}{2}$时,方程化为:t2+3=0,方程不成立,当$α≠\frac{π}{2}$时,由△=16cos2α-12=0,得${cos^2}α\;=\;\frac{3}{4}$,所以$cosα\;=\;\frac{{\sqrt{3}}}{2}$或$cosα\;=\;-\frac{{\sqrt{3}}}{2}$,
故直线l倾斜角α为$\frac{π}{6}$或$\frac{5π}{6}$.…(10分)
点评 本题考查参数方程与极坐标方程的应用,考查计算能力.

练习册系列答案
相关题目
10.已知tna2α=-$\frac{4}{3}$,α是第一象限角,则tanα等于( )
| A. | 1 | B. | 3 | C. | 4 | D. | 2 |
8.平面直角坐标系xOy中,已知向量$\overrightarrow{OA}$与$\overrightarrow{OB}$关于y轴对称,向量$\overrightarrow{a}$=(1,0),则满足$\overrightarrow{O{A}^{2}}$+$\overrightarrow{a}$$•\overrightarrow{AB}$=0的点A(x,y)的轨迹方程为( )
| A. | (x+1)2+y2=1 | B. | (x-1)2+y2=1 | C. | x2+y2=1 | D. | x2+(y-1)2=1 |
5.若程序框图如图所示,则该程序运行后输出k的值是( )


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
3.“α=$\frac{π}{4}$”是“tanα=1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
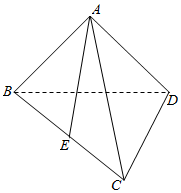 如图,在三棱锥A-BCD中,CD⊥BD,AB=AD,E为BC的中点.
如图,在三棱锥A-BCD中,CD⊥BD,AB=AD,E为BC的中点.