题目内容

将一颗骰子先后随机抛掷两次，设向上的点数分别为a，b，则使关于x的方程ax+b=0有整数解的概率为
 
．
考点：列举法计算基本事件数及事件发生的概率
专题：概率与统计
分析：据题意，将一颗骰子先后投掷两次共36种，x的方程ax+b=0有整数解，即为即b时a的倍数，一一列举出，再根据概率公式计算即可
解答： 解：根据题意，将一颗骰子先后投掷两次，得到的点数所形成的数组（a，b）有（1，1）、（1，2）、（1，3）、…、（6，6），共36种，
满足ax+b=0有整数解，即x=-
b
a
是整数，即b时a的倍数，有（1，1），（1，2），（1，3），（1，4），（1，5），（1，6），（2，2），（2，4），（2，6），（3，3），（3，6），（4，4），（5，5），（6，6）共14种，
故使关于x的方程ax+b=0有整数解的概率P=
14
36
=
7
18
，
故答案为：
7
18
点评：运用古典概型公式解题时需确定全部的基本事件的个数以及所求概率对应的基本事件数．
练习册系列答案
相关题目
已知数列{an}满足a2=2，Sn为其前n项和，且Sn=
an(n+1)
2
（n∈N*）．
（1）求a1的值；
（2）求证：an=
n
n-1
an-1（n≥2）；
（3）若bn=an•2 -an+1，求数列{bn}的前n项和Tn．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的短轴长为2，右焦点F与抛物线y2=4x的焦点重合．
（I）求椭圆C的标准方程；
（Ⅱ）过点(0，-
1
3
)且斜率为k的直线l与椭圆C交于A、B两点，求证：以AB为直径的圆必过y轴上的一定点M，并求出点M的坐标．
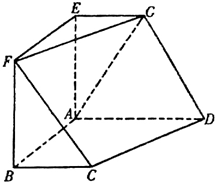如图，在六面体ABCDEFG中，平面EFG∥平面ABCD，AE⊥平面ABCD，EF⊥AE，AE=AB=AD，EG=BC，且EF=2EG．
（Ⅰ）求证：GD∥平面BCF；
（Ⅱ）求直线AG与平面GFCD所成角的正弦值．
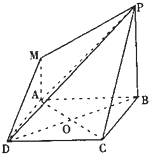如图，四边形ABCD是正方形，MA⊥平面ABCD，MA∥PB，PB=AB=2MA=2．
（1）P、C、D、M四点是否在同一平面内，为什么？
（2）求证：面PBD⊥面PAC；
（3）求直线BD和平面PMD所成角的正弦值．
已知圆A的方程为（x+1）2+y2=16，点B的坐标为（1，0），P是圆A上任意一点，线段BP的垂直平分线与AP交于点C．
（10求点C的轨迹方程；
（2）设直线x=-1与曲线C的一个交点为M，若在C上有两个动点E、F，且直线ME与MF关于直线x=-1对称，证明：直线EF的斜率为定值，并求出这个定值．
如图，在△ABC中，AF=
1
3
AB，D为BC的中点，AD与CF交于点E，若
AB
=
a
，
AC
=
b
，且
CE
=x
a
+y
b
，则x+y=
 
．
点P在双曲线
x
2
 
a
2
 
-
y
2
 
b
2
 
=1（a＞0，b＞0）上，F1，F2分别是双曲线的左、右焦点∠F1PF2=90°，且△F1PF2的三条边长之比为3：4：5．则双曲线的离心率是（　　）
A、
3
B、3
C、
5
D、5
已知函数f（x）的定义域为D．若对于任意的x1∈D，存在唯一的x2∈D，使得
f(x1)•f(x2)
=M成立，则称函数f（x）在D上的几何平均数为M．已知函数g（x）=3x+1（x∈[0，1]），则g（x）在区间[0，1]上的几何平均数为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网