题目内容

1．若三点A（1，3）、B（a，0）、C（0，1）共线，则a的值等于-$\frac{1}{2}$．

分析 三点A（1，3）、B（a，0）、C（0，1）共线，可得a≠0，1，kBA=kAC，利用斜率计算公式即可得出．

解答 解：三点A（1，3）、B（a，0）、C（0，1）共线，
则a≠0，1，kBA=kAC，可得$\frac{3-0}{1-a}$=$\frac{3-1}{1-0}$，解得a=-$\frac{1}{2}$．
故答案为：-$\frac{1}{2}$．

点评 本题考查了三点共线与斜率的关系，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
11．为了解高一学生对教师教学的意见，现将年级的500名学生编号如下：001，002，003，…，500，打算从中抽取一个容量为20的样本，按系统抽样的方法分成20个部分，如果第一部分编号为001，002，003，…025；第一部分用随机抽取一个号码为017，则抽取的第10个号码为242．
12．如图，已知四棱锥P-ABCD的底面是正方形，PD⊥底面ABCD
（Ⅰ）求证：AD∥平面PBC
（Ⅱ）求证：AC⊥平面PDB．
9．如果双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1上一点P到它的右焦点的距离是8，那么点P到它的左焦点的距离是4或12．
16．在平面直角坐标系xOy中，直线l的参数方程为$\left\{\begin{array}{l}{x=2+\frac{1}{2}t}\\{y=-\frac{\sqrt{3}}{2}t}\end{array}\right.$            （t为参数），以坐标原点O为极点，以x轴的正半轴为极轴，建立极坐标系，曲线C的极坐标方程为ρsin2θ=4cosθ．
（1）求曲线C和直线l的直角坐标系方程；
（2）设点P（2，0），直线l与曲线C交于A，B两点，求弦长|PA|•|PB|．
6．已知向量$\vec a=（2，x，3），\vec b=（-4，2，y）$，若$\vec a∥$$\vec b$则x+y=（　　）
A．-5B．0C．5D．-7
13．若随机变量ξ服从正态分布N（μ，σ2），P（μ-σ＜ξ＜μ+σ）=0.6826，P（μ-2σ＜ξ＜μ+2σ）=0.9544，设ξ～N（1，σ2），且P（ξ≥3）=0.1587，则σ=2．
10．方程$（x+y-1）\sqrt{{x^2}+{y^2}-4}=0$所表示的图形是（　　）
A．两条射线及一个圆B．两个点
C．一条线段及一个圆D．一条直线及一个圆
11．某程序框图如图所示，运行该程序输出的k值是（　　）
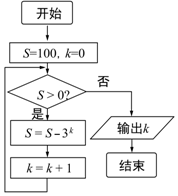
A．4B．5C．6D．7

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网