题目内容
已知f(x)=sinx-x,那么不等式f(a2)+f(2-3a)<0的解集为 .
考点:利用导数研究函数的单调性,函数单调性的性质
专题:函数的性质及应用
分析:本题直接求解是不可能的,因此可以研究函数的奇偶性与单调性,将原式化简成不含“f”符号的不等式,问题即可解决.
解答:
解:显然函数的定义域为R,又因为f(-x)=sin(-x)-x=-sinx-x=-(sinx+x)=-f(x),
所以该函数是奇函数,
而f′(x)=cosx-1≤0恒成立,且f′(x)=0的x不连续,
所以该函数在定义域内是单调减函数,
f(a2)+f(2-3a)<0可化为f(a2)<-f(2-3a)=f(3a-2)
所以a2>3a-2,即a2-3a+2>0,
解得a>2或a<1,
所以解集为{a|a>2或a<1}.
故答案为{a|a>2或a<1}.
所以该函数是奇函数,
而f′(x)=cosx-1≤0恒成立,且f′(x)=0的x不连续,
所以该函数在定义域内是单调减函数,
f(a2)+f(2-3a)<0可化为f(a2)<-f(2-3a)=f(3a-2)
所以a2>3a-2,即a2-3a+2>0,
解得a>2或a<1,
所以解集为{a|a>2或a<1}.
故答案为{a|a>2或a<1}.
点评:本题主要是考查了如何利用单调性求解不等式的思路,一般要结合奇偶性来用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
工人月工资(元)依劳动产值(千元)变化的回归直线方程为
=60+90x,下列判断正确的是( )
 |
| y |
| A、劳动产值为1 000元时,工资为50元 |
| B、劳动产值提高1 000元时,工资提高150元 |
| C、劳动产值提高1 000元时,工资提高90元 |
| D、劳动产值为1 000元时,工资为90元 |
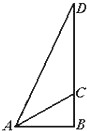 如图,某城市的电视发射塔CD建在市郊的小山上,小山的高BC为30m,在地面上有一点A,测得A、C间的距离为50米,从点A观测电视发射塔的视角为45°(∠CAD=45°),求这座电视发射塔的高度.
如图,某城市的电视发射塔CD建在市郊的小山上,小山的高BC为30m,在地面上有一点A,测得A、C间的距离为50米,从点A观测电视发射塔的视角为45°(∠CAD=45°),求这座电视发射塔的高度.