题目内容
9．
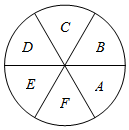如图所示，6个扇形区域A，B，C，D，E，F，现给这6个区域着色，要求同一个区域涂同一种颜色，相邻的两个区城不得使用同一种颜色，现有4种不同的颜色可用，那么一共有多少种不同的涂色方法？
分析 对相间区域A、C、E，分类讨论，即可得出结论．
解答 解：（1）当相间区域A、C、E着同一种颜色时，有4种着色方法，此时，B、D、F各有3种着色方法，故有4×3×3×3=108 种方法．
（2）当相间区域A、C、E着色两不同的颜色时，有 4×3×3=36种着色方法，此时B、D、F有 3×2×2=12种着色方法，故共有 432 种着色方法．
（3）当相间区域A、C、E着三种不同的颜色时有 4×3×2=24 种着色方法，此时B、D、F各有2种着色方法．此时共有 24×2×2×2=192种方法．
故总计有108+432+192=732种方法．
点评 本题考查理解题意能力，考查分类思想的运用，考查学生分析解决问题的能力，属于基础题．
练习册系列答案
相关题目
19．已知正四面体ABCD，点E，F分别为棱AB，AC的中点，球O是正四面体ABCD的外接球，球O截直线EF所得的弦长为6$\sqrt{5}$，则正四面体的棱长为（ ）
| A． | 6$\sqrt{5}$ | B． | 12 | C． | 6$\sqrt{3}$ | D． | 6$\sqrt{2}$ |
18．某台机床加工的1000只产品中次品数的频率分布如表，则次品数的众数、平均数依次为0和5，3.4．．
| 次品数 | 0 | 1 | 2 | 3 | 5 |
| 频率 | 0.5 | 0.2 | 0.05 | 0.2 | 0.5 |
如图，圆x2+y2=8内有一点P（-1，2），AB为过点P的弦．