题目内容
19.已知{an}是等比数列,{bn}是首项为1,公差d大于零的等差数列,且满足a1b1=3,a2b2=27,a3b3=135.(1)求数列{an},{bn}的通项公式;
(2)求a1b1+a2b2+…+anbn.
分析 (1)设{an}是公比为q的等比数列,运用等差数列和等比数列的通项公式,解方程可得公比和公差,即可得到所求通项公式;
(2)运用数列的求和方法:错位相减法,结合等比数列的求和公式,即可得到所求和.
解答 解:(1)设{an}是公比为q的等比数列,
由a1b1=3,a2b2=27,a3b3=135,
可得a1=3,3q(1+d)=27,3q2(1+2d)=135,
解得q=3,d=2,
即有an=a1qn-1=3•3n-1=3n;
bn=b1+(n-1)d=1+2(n-1)=2n-1;
(2)令Sn=a1b1+a2b2+…+anbn=1•3+3•32+5•33+…+(2n-1)•3n,
3Sn=1•32+3•33+5•34+…+(2n-1)•3n+1,
相减可得-2Sn=3+2(32+33+…+3n)-(2n-1)•3n+1
=3+2•$\frac{9(1-{3}^{n-1})}{1-3}$-(2n-1)•3n+1,
化简可得Sn=(n-1)•3n+1+3.
点评 本题考查等差数列和等比数列的通项公式的运用,考查数列的求和方法:错位相减法,同时考查等比数列的求和公式的运用,属于中档题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
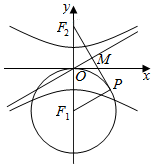 如图,已知F1,F2是双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\;(a>0,b>0)$的下,上焦点,过F2点作以F1为圆心,|OF1|为半径的圆的切线,P为切点,若切线段PF2被一条渐近线平分,则双曲线的离心率为( )
如图,已知F1,F2是双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\;(a>0,b>0)$的下,上焦点,过F2点作以F1为圆心,|OF1|为半径的圆的切线,P为切点,若切线段PF2被一条渐近线平分,则双曲线的离心率为( )