题目内容
14.如图,边长为2的正方形ABCD中,点E、点F分别是AB、BC上的点,且BE=BF,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A1.(Ⅰ)若点E是边AB的中点,求证:A1D⊥EF;
(Ⅱ)当$BE=\frac{1}{2}$时,求三棱锥A1-DEF的体积.
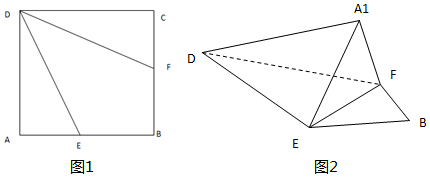
分析 (Ⅰ)折叠前有AD⊥AE,CD⊥CF,折叠后有A1D⊥A1E,A1D⊥A1F,从而A1D⊥平面A1EF,由此能证明A1D⊥EF.
(Ⅱ)取EF的中点O,连接A1O,三棱锥A1-DEF的体积${V_{{A_1}-EFD}}=\frac{1}{3}•{S_{△E{A_1}F}}•{A_1}D$,由此能求出结果.
解答 解::(Ⅰ)折叠前有AD⊥AE,CD⊥CF,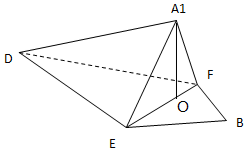
折叠后有A1D⊥A1E,A1D⊥A1F,
又A1E∩A1F=A1,∴A1D⊥平面A1EF,
∴A1D⊥EF.…(6分)
解:(Ⅱ)由正方形ABCD的边长为2,
折叠后A1D=2,${A_1}E={A_1}F=\frac{3}{2}$,$EF=\frac{{\sqrt{2}}}{2}$,
取EF的中点O,连接A1O,
则${A_1}O=\sqrt{{A_1}{E^2}-E{O^2}}=\frac{{\sqrt{34}}}{4}$
∴${S_{△E{A_1}F}}=\frac{1}{2}•{A_1}O•EF=\frac{{\sqrt{17}}}{8}$,
∴${V_{{A_1}-EFD}}=\frac{1}{3}•{S_{△E{A_1}F}}•{A_1}D=\frac{{\sqrt{17}}}{12}$.…(12分)
点评 本题考查柱、锥、台体的体积,解答此题的关键是注意折叠问题在折叠前后的变量与不变量,考查空间想象能力与计算能力,是中档题.

练习册系列答案
相关题目
5.已知非零向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a-\overrightarrow b}|=2,|{\overrightarrow a}|=1$,则$\overrightarrow a+\overrightarrow b$与$\overrightarrow a-\overrightarrow b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
9.设函数f(x)=2sinπx与函数$y=\frac{1}{1-x}$的图象在区间[-2,4]上交点的横坐标依次分别为x1,x2,…,xn,则$\sum_{i=1}^{n}$xi=( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
6.某商场计划销售某种产品,现邀请生产该产品的甲、乙两个厂家进场试销10天.两个厂家提供的返利方案如下:甲厂家每天固定返利70元,且每卖出一件产品厂家再返利2元;乙厂家无固定返利,卖出40件以内(含40件)的产品,每件产品厂家返利4元,超出40件的部分每件返利6元.经统计,两个厂家的试销情况茎叶图如下:
(Ⅰ)现从甲厂家试销的10天中抽取两天,求这两天的销售量都大于40的概率;
(Ⅱ)若将频率视作概率,回答以下问题:
(ⅰ)记乙厂家的日返利额为X(单位:元),求X的分布列和数学期望;
(ⅱ)商场拟在甲、乙两个厂家中选择一家长期销售,如果仅从日返利额的角度考虑,请利用所学的统计学知识为商场作出选择,并说明理由.
| 甲 | 乙 | ||||||||||||
| 8 | 9 | 9 | 8 | 9 | 9 | 3 | 8 | 9 | 9 | ||||
| 2 | 0 | 1 | 0 | 4 | 2 | 1 | 1 | 1 | 0 | 1 | 0 | ||
(Ⅱ)若将频率视作概率,回答以下问题:
(ⅰ)记乙厂家的日返利额为X(单位:元),求X的分布列和数学期望;
(ⅱ)商场拟在甲、乙两个厂家中选择一家长期销售,如果仅从日返利额的角度考虑,请利用所学的统计学知识为商场作出选择,并说明理由.
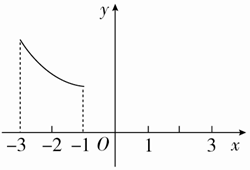 定义在[-3,-1]∪[1,3]上的函数y=f(x)是奇函数,其部分图象如图所示.
定义在[-3,-1]∪[1,3]上的函数y=f(x)是奇函数,其部分图象如图所示.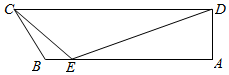 如图,在平面四边形ABCD中,已知∠A=$\frac{π}{2}$,∠B=$\frac{2π}{3}$,AB=6,在AB边上取点E,使得BE=1,连接EC,ED.若∠CED=$\frac{2π}{3}$,EC=$\sqrt{7}$.
如图,在平面四边形ABCD中,已知∠A=$\frac{π}{2}$,∠B=$\frac{2π}{3}$,AB=6,在AB边上取点E,使得BE=1,连接EC,ED.若∠CED=$\frac{2π}{3}$,EC=$\sqrt{7}$.