题目内容
16．已知点P（2，0），及⊙C：x2+y2-6x+4y+4=0．当直线L过点P且与圆心C的距离为1时，求直线L的方程．分析 利用分类讨论，利用直线与圆的圆心的距离列出方程，分别求解即可．
解答 解：设直线l的斜率为k（k存在）则方程为y-0=k（x-2），
又⊙C：x2+y2-6x+4y+4=0的圆心为（3，-2），
r=3由$\frac{|3k-2k+2|}{\sqrt{{k}^{2}+1}}=1$，可得k=$-\frac{3}{4}$，所以直线方程为y=-$\frac{3}{4}（x-2）$，
即：3x+4y-6=0，
当k不存在时，l的方程为x=2．
点评 本题考查直线与圆的位置关系的应用，考查点到直线的距离公式的应用，考查计算能力．
练习册系列答案
相关题目
如图在正方体ABCD-A1B1C1D1中，E是棱CC1的中点．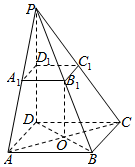
在四棱锥P-ABCD中，底面ABCD是菱形，PD⊥平面ABCD，点D1为棱PD的中点，过D1作与平面ABCD平行的平面与棱PA，PB，PC相交于A1，B1，C1，∠BAD=60°．