题目内容

9．在等差数列{an}中，Sn为它的前n项和，若a1＞0，S16＞0，S17＜0，则当Sn最大时，n的值为（　　）
A．7B．8C．9D．10

分析 根据所给的等差数列的S16＞0且S17＜0，根据等差数列的前n项和公式，看出第9项小于0，第8项和第9项的和大于0，得到第8项大于0，这样前8项的和最大．

解答 解：∵等差数列{an}中，S16＞0且S17＜0，
即S16=$\frac{16{（a}_{1}+{a}_{16}）}{2}=8（{a}_{8}+{a}_{9}）＞0$，
S17=$\frac{17（{a}_{1}+{a}_{17}）}{2}$=17a9＜0，
∴a8+a9＞0，a9＜0，
∴a8＞0，
∴数列的前8项和最大．
故答案为：8．

点评 本题考查等差数列的性质和前n项和，以及等差数列的性质，解题的关键是熟练运用等差数列的性质得出已知数列的项的正负．

练习册系列答案
相关题目
19．已知函数f（x）=$\left\{{\begin{array}{l}{{x^2}+x+a，x＜0}\\{-\frac{1}{x}，x＞0}\end{array}}$，的图象上存在不同的两点A，B，使得曲线y=f（x）在这两点处的切线重合，则实数a的取值范围是（　　）
A．（-∞，$\frac{1}{4}$）B．（2，+∞）C．（-2，$\frac{1}{4}$）D．（-∞，2）∪（$\frac{1}{4}$，+∞）
20．已知命题p：双曲线$\frac{y^2}{5}-\frac{x^2}{m}$=1的离心率$e∈（\frac{{\sqrt{6}}}{2}，\sqrt{2}）$，命题q：方程$\frac{x^2}{2m}+\frac{y^2}{9-m}$=1表示焦点在x轴上的椭圆，若“p或q”为真命题，“p且q”为假命题，求实数m的取值范围．
17．若抛物线y2=8x上有一点P，它到焦点的距离为20，则P点的横坐标为18．
4．已知数列{an}中，a1=1，an+1=2an+3，数列{bn}中，b1=1，且点（bn+1，bn）在直线y=x-1上．
（Ⅰ） 求数列{an}的通项公式；     
（Ⅱ）求数列{bn}的通项公式；
（Ⅲ）求数列{bn}的前n项和Sn．
14．函数$f（x）=cos（3x+\frac{5π}{2}）$，满足$\frac{f（{x}_{i}）}{{x}_{i}}=m$，其中${x}_{i}∈[-2π，2π]，i=1，2，…，n，n∈{N}^{*}$，则n的最大值为（　　）
A．13B．12C．10D．8
1．以直角坐标系的原点O为极点，x轴的正半轴为极轴，且两个坐标系取相同的单位长度，已知直线I的参数方程为$\left\{\begin{array}{l}x=1+t\\ y=1+\sqrt{3}t\end{array}\right.$（t为参数），圆C的极坐标方程为ρ=2，点P关于极点对称的点P'QUOTE p?的极坐标为$（\sqrt{2}，\frac{5π}{4}）$（1）写出圆C的直角坐标方程及点P的极坐标；
（2）设直线I与圆C相交于两点A、B，求点P到A、B两点的距离之积．
18．设X-B（10，0.8），则D（2X+1）等于（　　）
A．1.6B．3.2C．6.4D．12.8
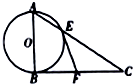14．如图，在△ABC中，∠ABC=90°，以AB为直径的圆交AC于点E，过点E作圆O的切线交BC于点F．
（1）求证：BC=2EF；
（2）若CE=3OA，求∠EFB的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网