题目内容
18．已知函数$f（x）=a{x^3}-bx+\frac{c}{x}+2．f（-2）=7，则f（2）$=（ ）| A． | 5 | B． | -7 | C． | 3 | D． | -3 |
分析 利用已知条件集合函数的奇偶性求解即可．
解答 解：$f（x）=a{x}^{3}-bx+\frac{c}{x}+2．f（-2）=7$，
可得$f（-2）=-8a+2b-\frac{c}{2}+2=7$，
$8a-2b+\frac{c}{2}=-5$，
f（2）=$8a-2b+\frac{c}{2}+2=-5+2=-3$．
故选：D．
点评 本题考查函数的函数式的应用，函数的奇偶性的应用，是基础题．
练习册系列答案
相关题目
8．一个弹性小球从10米自由落下，着地后反弹到原来高度的$\frac{4}{5}$处，再自由落下，又弹回到上一次高度的$\frac{4}{5}$处，假设这个小球能无限次反弹，则这个小球在这次运动中所经过的总路程为（ ）
| A． | 50 | B． | 80 | C． | 90 | D． | 100 |
9．直线4x-3y=0与圆x2+y2=36的位置关系是（ ）
| A． | 相交 | B． | 相离 | C． | 相切 | D． | 不能确定 |
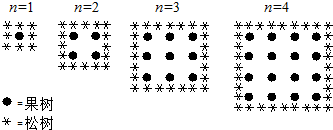某农场规划将果树种在正方形的场地内．为了保护果树不被风吹，决定在果树的周围种松树． 在如图里，你可以看到规划种植果树的列数（n），果树数量及松树数量的规律：