题目内容
已知x∈(0,π),cos(
-x)=
,则tanx= .
| π |
| 4 |
| ||
| 10 |
考点:两角和与差的正切函数,同角三角函数基本关系的运用
专题:三角函数的求值
分析:由和差角的公式化简可得cosx+sinx=
,结合cos2x+sin2x=1和x的范围可得sinx和cosx的值,可得tanx.
| 1 |
| 5 |
解答:
解:∵cos(
-x)=
,
∴
cosx+
sinx=
,
∴cosx+sinx=
,
又cos2x+sin2x=1,x∈(0,π),
∴sinx>0,
联立解得sinx=
,cosx=-
,
∴tanx=
=-
| π |
| 4 |
| ||
| 10 |
∴
| ||
| 2 |
| ||
| 2 |
| ||
| 10 |
∴cosx+sinx=
| 1 |
| 5 |
又cos2x+sin2x=1,x∈(0,π),
∴sinx>0,
联立解得sinx=
| 4 |
| 5 |
| 3 |
| 5 |
∴tanx=
| sinx |
| cosx |
| 4 |
| 3 |
点评:本题考查同角三角函数的基本关系,以及和差角的三角函数公式,属基础题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
在复平面内,若复数z=(x2-9)+(x-3)i为纯虚数,则实数x值为( )
| A、-3 | B、0 | C、3 | D、-3或3 |
 E为圆内两弦AB和CD的交点,过点E作AD的平行线交BC的延长线于点F.
E为圆内两弦AB和CD的交点,过点E作AD的平行线交BC的延长线于点F.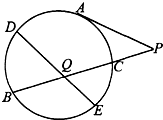 如图,PA为圆的切线,切点为A,割线PCB与圆相交于B、C两点,弦DE经过弦BC的中点Q,若AP=3
如图,PA为圆的切线,切点为A,割线PCB与圆相交于B、C两点,弦DE经过弦BC的中点Q,若AP=3