题目内容
19.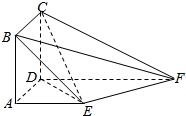 如图,四边形ABCD为正方形,四边形AEFD为梯形,FD∥EA,FD⊥平面ABCD,FD=2EA=2AD.
如图,四边形ABCD为正方形,四边形AEFD为梯形,FD∥EA,FD⊥平面ABCD,FD=2EA=2AD.(Ⅰ)证明:平面EFC⊥平面DCE;
(Ⅱ)求直线CE与平面BDE所成角的正弦值.
分析 (I)根据线面垂直的判定可证EF⊥平面DCE,即可证明平面EFC⊥平面DCE;
(II)建立坐标系,利用向量法求直线CE与平面BDE所成角的正弦值.
解答 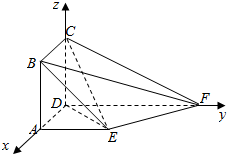 (I)证明:由已知:FD⊥平面ABCD,∴FD⊥CD.
(I)证明:由已知:FD⊥平面ABCD,∴FD⊥CD.
∵CD⊥AD,AD∩FD=D,
∴CD⊥平面AEFD,∴EF⊥CD,
设FD=2EA=2AD=2,∴DE=EF=$\sqrt{2}$,
∴DF2=DE2+EF2,
∴EF⊥ED,
∵CD∩ED=D,∴EF⊥平面DCE,
∵EF?平面EFC,
∴平面EFC⊥平面DCE;
(Ⅱ)解:以DA,DF,DC为x,y,z轴,建立如图所示的坐标系,设AD=1,则D(0,0,0),B(1,0,1),E(1,1,0),C(0,0,1),
∴$\overrightarrow{CE}$=(1,1,-1),$\overrightarrow{DB}$=(1,0,1),$\overrightarrow{DE}$=(1,1,0),
设平面BDE的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{x+z=0}\\{x+y=0}\end{array}\right.$,
取$\overrightarrow{n}$=(1,-1,-1),
∴直线CE与平面BDE所成角的正弦值=|$\frac{1-1+1}{\sqrt{3}•\sqrt{3}}$|=$\frac{1}{3}$.
点评 本题考查线面、面面垂直的判定,考查线面角,考查向量知识的运用,属于中档题.

练习册系列答案
相关题目
9.下列四个函数中,在(0,+∞)上为增函数的是( )
| A. | f(x)=3-x | B. | f(x)=-$\frac{1}{x+1}$ | C. | f(x)=x2-3x | D. | f(x)=-|x| |
10.若直线x+2y+1=0与直线ax+y-2=0互相垂直,那么a的值等于( )
| A. | -2 | B. | -$\frac{2}{3}$ | C. | -$\frac{1}{3}$ | D. | 1 |
11.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增,若实数a满足f(lga)+f(lg$\frac{1}{a}$)≤2f(1),则a的取值范围是( )
| A. | (-∞,10] | B. | [$\frac{1}{10}$,10] | C. | (0,10] | D. | [$\frac{1}{10}$,1] |
8.在圆x2+y2-2x-6y=15内,过点E(0,1)的最长弦和最短弦分别是AC和BD,则|AC|•|BD|的值为( )
| A. | $80\sqrt{5}$ | B. | $60\sqrt{5}$ | C. | $40\sqrt{5}$ | D. | $20\sqrt{5}$ |
9.设x∈{-1,1},y∈{-2,0,2},则以(x,y)为坐标的点落在不等式x+2y≥1所表示的平面区域内的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |