题目内容
7.已知等差数列{an},公差为2,的前n项和为Sn,且a1,S2,S4成等比数列,(1)求数列{an}的通项公式;
(2)设bn=$\frac{2}{{a}_{n}•{a}_{n+1}}$(n∈N*),求数列{bn}的前n项和Tn.
分析 (1))由a1,S2,S4成等比数列得${S_2}^2={a_1}{S_4}$.化简解得a1,再利用等差数列的通项公式即可得出;
(2)利用“裂项求和”即可得出.
解答 解:(1))由a1,S2,S4成等比数列得${S_2}^2={a_1}{S_4}$.
化简得${(2{a_1}+d)^2}={a_1}(4{a_1}+6d)$,又d=2,解得a1=1,
故数列{an}的通项公式${a_n}=1+2(n-1)=2n-1(n∈{N^*})$…(5分)
(2)∵${b_n}=\frac{2}{{{a_n}{a_{n+1}}}}$∴由(1)得${b_n}=\frac{2}{(2n-1)(2n+1)}=\frac{1}{2n-1}-\frac{1}{2n+1}$,
∴${T_n}=(1-\frac{1}{3})+(\frac{1}{3}-\frac{1}{5})+(\frac{1}{5}-\frac{1}{6})+…+(\frac{1}{2n-1}-\frac{1}{2n+1})$=$1-\frac{1}{2n+1}=\frac{2n}{2n+1}(n∈{N^*})$…(10分).
点评 本题考查了等差数列的通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.函数y=|log2x|-2-x的零点个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.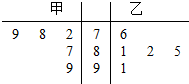 将甲,乙两名同学5次数学测验的成绩用茎叶图表示如图,若甲,乙两人成绩的中位数分别是x甲,x乙,则下列说法正确的是( )
将甲,乙两名同学5次数学测验的成绩用茎叶图表示如图,若甲,乙两人成绩的中位数分别是x甲,x乙,则下列说法正确的是( )
 将甲,乙两名同学5次数学测验的成绩用茎叶图表示如图,若甲,乙两人成绩的中位数分别是x甲,x乙,则下列说法正确的是( )
将甲,乙两名同学5次数学测验的成绩用茎叶图表示如图,若甲,乙两人成绩的中位数分别是x甲,x乙,则下列说法正确的是( )| A. | x甲<x乙,乙比甲成绩稳定 | B. | x甲>x乙;甲比乙成绩稳定 | ||
| C. | x甲>x乙;乙比甲成绩稳定 | D. | x甲<x乙;甲比乙成绩稳定 |
2.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,x>0}\\{{a}^{x},a>0,x≤0}\end{array}\right.$若f(f($\frac{1}{4}$))=4,则a=( )
| A. | $\frac{1}{4}$ | B. | 4 | C. | $\frac{1}{2}$ | D. | 2 |
16.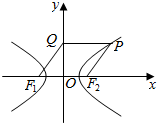 已知点P在以F1,F2为焦点的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上,过P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该双曲线的离心率为( )
已知点P在以F1,F2为焦点的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上,过P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该双曲线的离心率为( )
 已知点P在以F1,F2为焦点的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上,过P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该双曲线的离心率为( )
已知点P在以F1,F2为焦点的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上,过P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该双曲线的离心率为( )| A. | $\frac{1+\sqrt{2}}{2}$ | B. | $\frac{1+\sqrt{3}}{2}$ | C. | 1$+\sqrt{2}$ | D. | 1+$\sqrt{3}$ |
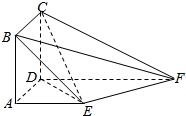 如图,四边形ABCD为正方形,四边形AEFD为梯形,FD∥EA,FD⊥平面ABCD,FD=2EA=2AD.
如图,四边形ABCD为正方形,四边形AEFD为梯形,FD∥EA,FD⊥平面ABCD,FD=2EA=2AD.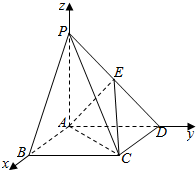 已知正方形ABCD的边长为2,PA⊥平面ABCD,且PA=2,E是PD中点.以A为原点,建立如图所示的空间直角坐标系A-xyz.
已知正方形ABCD的边长为2,PA⊥平面ABCD,且PA=2,E是PD中点.以A为原点,建立如图所示的空间直角坐标系A-xyz.