题目内容
11.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增,若实数a满足f(lga)+f(lg$\frac{1}{a}$)≤2f(1),则a的取值范围是( )| A. | (-∞,10] | B. | [$\frac{1}{10}$,10] | C. | (0,10] | D. | [$\frac{1}{10}$,1] |
分析 根据函数的奇偶数和单调性之间的关系,将不等式进行等价转化即可得到结论.
解答 解:∵函数f(x)是定义在R上的偶函数,
∴f(lga)+f(lg$\frac{1}{a}$)≤2f(1),等价为f(lga)+f(-lga)=2f(lga)≤2f(1),
即f(lga)≤f(1).
∵函数f(x)是定义在R上的偶函数,且在区间[0,+∞)单调递增,
∴f(lga)≤f(1)等价为f(|lga|)≤f(1).
即|lga|≤1,
∴-1≤lga≤1,
解得$\frac{1}{10}$≤a≤10,
故选:B.
点评 本题主要考查对数的基本运算以及函数奇偶性和单调性的应用,综合考查函数性质的综合应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,x>0}\\{{a}^{x},a>0,x≤0}\end{array}\right.$若f(f($\frac{1}{4}$))=4,则a=( )
| A. | $\frac{1}{4}$ | B. | 4 | C. | $\frac{1}{2}$ | D. | 2 |
6.在直角坐标系中,下列直线中倾斜角为钝角的是( )
| A. | y=3x-1 | B. | x+2=0 | C. | $\frac{x}{2}$+$\frac{y}{3}$=1 | D. | 2x-y+1=0 |
16.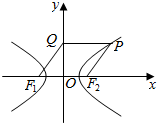 已知点P在以F1,F2为焦点的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上,过P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该双曲线的离心率为( )
已知点P在以F1,F2为焦点的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上,过P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该双曲线的离心率为( )
 已知点P在以F1,F2为焦点的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上,过P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该双曲线的离心率为( )
已知点P在以F1,F2为焦点的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上,过P作y轴的垂线,垂足为Q,若四边形F1F2PQ为菱形,则该双曲线的离心率为( )| A. | $\frac{1+\sqrt{2}}{2}$ | B. | $\frac{1+\sqrt{3}}{2}$ | C. | 1$+\sqrt{2}$ | D. | 1+$\sqrt{3}$ |
20.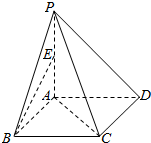 四棱锥P-ABCD的底面是一个正方形,PA⊥平面ABCD,PA=AB=2,E是棱PA的中点,则异面直线BE与AC所成角的余弦值是( )
四棱锥P-ABCD的底面是一个正方形,PA⊥平面ABCD,PA=AB=2,E是棱PA的中点,则异面直线BE与AC所成角的余弦值是( )
 四棱锥P-ABCD的底面是一个正方形,PA⊥平面ABCD,PA=AB=2,E是棱PA的中点,则异面直线BE与AC所成角的余弦值是( )
四棱锥P-ABCD的底面是一个正方形,PA⊥平面ABCD,PA=AB=2,E是棱PA的中点,则异面直线BE与AC所成角的余弦值是( )| A. | $\frac{{\sqrt{15}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
1.已知点A(0,0,0),B(1,0,1),C(0,1,1),则平面ABC的一个法向量$\overrightarrow m$是( )
| A. | (1,1,1) | B. | (1,1,-1) | C. | (-1,1,1) | D. | (1,-1,1) |
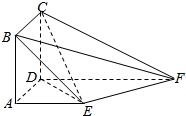 如图,四边形ABCD为正方形,四边形AEFD为梯形,FD∥EA,FD⊥平面ABCD,FD=2EA=2AD.
如图,四边形ABCD为正方形,四边形AEFD为梯形,FD∥EA,FD⊥平面ABCD,FD=2EA=2AD.