题目内容
先解答(1),再通过结构类比解答(2):
(1)请用tanx表示tan(x+
),并写出函数y=tan(x+
)的最小正周期;
(2)设x∈R,a为非零常数,且f(x+2a)=
,试问f(x)是周期函数吗?证明你的结论.
(1)请用tanx表示tan(x+
| π |
| 4 |
| π |
| 4 |
(2)设x∈R,a为非零常数,且f(x+2a)=
| 1+f(x) |
| 1-f(x) |
考点:两角和与差的正切函数,三角函数的周期性及其求法
专题:三角函数的求值
分析:(1)由两角和的正切公式可得示tan(x+
),易得函数的周期;(2)类比可得f(x)是以8a为其一个周期的周期函数,由周期的定义证明即可.
| π |
| 4 |
解答:
解:(1)由两角和的正切公式可得tan(x+
)=
=
;
函数y=tan(x+
)的最小正周期为π;
(2)f(x)是以8a为其一个周期的周期函数,下面证明:
∵f(x+4a)=f((x+2a)+2a)=
=
=-
,
∴f(x+8a)=f((x+4a)+4a)=-
=-
=f(x),
∴f(x)是周期函数,其中一个周期为8a
| π |
| 4 |
tanx+tan
| ||
1-tanxtan
|
| 1+tanx |
| 1-tanx |
函数y=tan(x+
| π |
| 4 |
(2)f(x)是以8a为其一个周期的周期函数,下面证明:
∵f(x+4a)=f((x+2a)+2a)=
| 1+f(x+2a) |
| 1-f(x+2a) |
1+
| ||
1-
|
| 1 |
| f(x) |
∴f(x+8a)=f((x+4a)+4a)=-
| 1 |
| f(x+4a) |
| 1 | ||
-
|
∴f(x)是周期函数,其中一个周期为8a
点评:本题考查两角和与差的正切函数,涉及三角函数的周期性,属中档题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
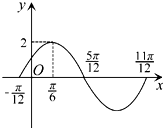 函数y=2sin(ωx+φ)(ω>0,|φ|<
函数y=2sin(ωx+φ)(ω>0,|φ|<