题目内容
证明:f(x)=
在(0,+∞)上是减函数.
| 1 |
| x2 |
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:先求出函数的导数,由导数值小于0,得出函数是减函数.
解答:
证明:∵f(x)=
,(x>0),
∴f′x)=-
<0,
∴f(x)=
在(0,+∞)上是减函数.
| 1 |
| x2 |
∴f′x)=-
| 2 |
| x3 |
∴f(x)=
| 1 |
| x2 |
点评:本题考察了函数的单调性,导数的应用,是一道基础题.

练习册系列答案
相关题目
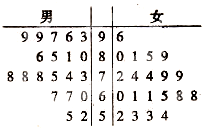 在某次数学考试中,从高一年级300名男生和300名女生中,各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示:
在某次数学考试中,从高一年级300名男生和300名女生中,各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示: