题目内容
“a2+b2＞0”是“ab≠0”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据不等式的性质，结合充分条件和必要条件的定义即可得到结论．
解答：
解：当a=0，b≠0时，满足a2+b2＞0，但ab≠0不成立，即充分性不成立，
若ab≠0，则a2+b2＞0成立，即充分性成立，
故“a2+b2＞0”是“ab≠0”的必要不充分条件，
故选：B
若ab≠0，则a2+b2＞0成立，即充分性成立，
故“a2+b2＞0”是“ab≠0”的必要不充分条件，
故选：B
点评：本题主要考查充分条件和必要条件的判断，根据不等式的性质是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
在下列函数中，奇函数是（ ）
| A、f（x）=1-x2 |
| B、f（x）=x3 |
| C、f（x）=2x |
| D、f（x）=x+1 |
已知点A（1，2），B（3，1），则线段AB的垂直平分线的方程为（ ）
| A、4x+2y-5=0 |
| B、4x-2y-5=0 |
| C、x+2y-5=0 |
| D、x-2y-5=0 |
在复平面内，复数z=1-i对应于点P，则该点在以原点为极点，实轴的正半轴为极轴的极坐标系中所对应的极坐标是（ ）
A、(
| ||||
B、(2，
| ||||
C、(
| ||||
D、(2，
|
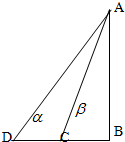如图：D，C，B三点在地面同一直线上，DC=a，从C，D两点测得A点仰角分别是β，α（α＜β），则A点离地面的高度AB等于