题目内容
【题目】已知函数![]() ,
,![]() 为其导函数.
为其导函数.
(Ⅰ)当![]() ,
,![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(Ⅱ)设![]() ,当
,当![]() 时,对任意的
时,对任意的![]() ,都有
,都有![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() 极大值
极大值![]() ,
,![]() 极小值
极小值![]() .(Ⅱ)
.(Ⅱ)![]()
【解析】
(Ⅰ)研究函数的极值情况,应由导函数的正负确定函数的单调区间,明确函数的单调性确定极值点即可;(Ⅱ)存在性与任意性问题应转化为相关函数的最值求解,特别地如果所研究的函数为含参的二次函数时,应从运动观点上分析,确定对称轴在目标区间内外时的对应函数图象即可求解.
解:(Ⅰ)函数![]() 的定义域为
的定义域为![]() ,且
,且![]() ,
,
由题意,当![]() ,
,![]() 时,
时,
由![]() ,得
,得![]() 或
或![]() .
.![]() 得
得![]() .
.
故![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() 极大值
极大值![]() ,
,
![]() 极小值
极小值![]() .
.
(Ⅱ)![]() ,
,![]() ,有
,有![]() 恒成立,
恒成立,
即![]() .
.
因为![]() ,则
,则![]() ,
,
若![]() ,
,![]() ,
,![]() ;
;
若![]() ,在
,在![]() 的对称轴为
的对称轴为![]() ,
,
故当![]() ,即
,即![]() 时,
时,
![]() ;
;
当![]() 即
即![]() 时,
时,
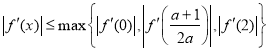
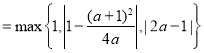 ,
,
又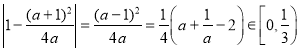 ,
,
![]() ,所以
,所以![]() .
.
综上所述,![]() ,
,
因此![]() ,即
,即![]() 的取值范围为
的取值范围为![]()

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目