Question

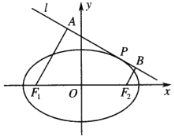
【题目】已知椭圆经过点，离心率为

（1）求椭圆的方程；

（2）设直线与椭圆相交于，两点，若以，为邻边的平行四边形的顶点在椭圆上，求证：平行四边形的面积为定值.

Answer 1

【答案】（1）（2）证明见解析；

【解析】

（1）由题意可得关于的方程组，求得的值，则椭圆方程可求；
（2）联立直线方程与椭圆方程，化为关于的一元二次方程，利用根与系数的关系及四边形是平行四边形，可得点坐标，把点坐标代入椭圆方程，得到，利用弦长公式求得，再由点到直线的距离公式求出点到直线的距离，代入三角形面积公式即可证明平行四边形的面积为定值．

解：（1）因为椭圆过点，代入椭圆方程，可得①，

又因为离心率为，所以，从而②，

联立①②，解得，，

所以椭圆为；

（2）把代入椭圆方程，

得，

所以，

设，，则，

所以，

因为四边形是平行四边形，

所以，

所以点坐标为.

又因为点在椭圆上，

所以，即.

因为

.

又点到直线的距离，

所以平行四边形的面积

，

即平行四边形的面积为定值.