题目内容
已知函数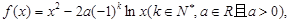
(1)讨论函数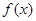 的单调性;
的单调性;
(2)若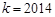 时,关于
时,关于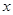 的方程
的方程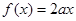 有唯一解,求
有唯一解,求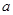 的值;
的值;
(3)当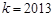 时,证明: 对一切
时,证明: 对一切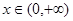 ,都有
,都有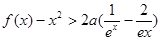 成立.
成立.
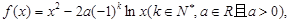
(1)讨论函数
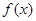 的单调性;
的单调性;(2)若
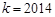 时,关于
时,关于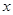 的方程
的方程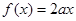 有唯一解,求
有唯一解,求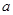 的值;
的值;(3)当
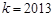 时,证明: 对一切
时,证明: 对一切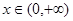 ,都有
,都有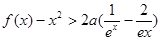 成立.
成立.(1)当k是奇数时, f(x)在(0,+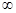 )上是增函数;
)上是增函数;
当k是偶数时,f (x)在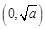 上是减函数,在
上是减函数,在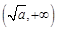 上是增函数.
上是增函数.
(2)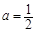
(3)当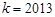 时, 问题等价于证明
时, 问题等价于证明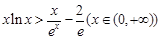
由导数可求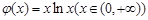 的最小值是
的最小值是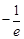 ,当且仅当
,当且仅当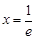 时取到,
时取到,
设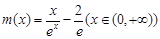 ,利用导数求解。
,利用导数求解。
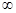 )上是增函数;
)上是增函数; 当k是偶数时,f (x)在
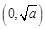 上是减函数,在
上是减函数,在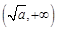 上是增函数.
上是增函数.(2)
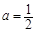
(3)当
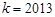 时, 问题等价于证明
时, 问题等价于证明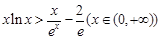
由导数可求
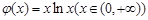 的最小值是
的最小值是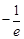 ,当且仅当
,当且仅当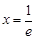 时取到,
时取到, 设
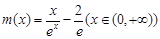 ,利用导数求解。
,利用导数求解。试题分析:(1)由已知得x>0且
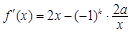 .
.当k是奇数时,
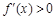 ,则f(x)在(0,+
,则f(x)在(0,+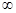 )上是增函数;
)上是增函数; 当k是偶数时,则
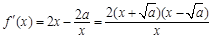 .
. 所以当x
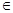
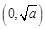 时,
时,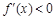 ,当x
,当x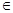
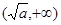 时,
时,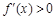 .
. 故当k是偶数时,f (x)在
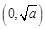 上是减函数,在
上是减函数,在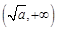 上是增函数.…………4分
上是增函数.…………4分(2)若
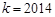 ,则
,则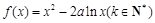 .
.记

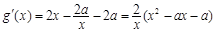 ,
,若方程f(x)=2ax有唯一解,即g(x)=0有唯一解; 令
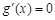 ,得
,得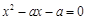 .因为
.因为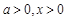 ,所以
,所以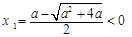 (舍去),
(舍去),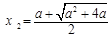 . 当
. 当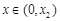 时,
时,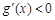 ,
,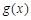 在
在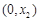 是单调递减函数;
是单调递减函数;当
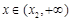 时,
时,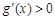 ,
,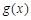 在
在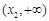 上是单调递增函数.
上是单调递增函数.当x=x2时,
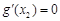 ,
,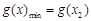 . 因为
. 因为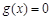 有唯一解,所以
有唯一解,所以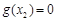 .
.则
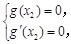 即
即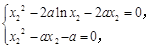 设函数
设函数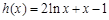 ,
,因为在x>0时,h (x)是增函数,所以h (x) = 0至多有一解.
因为h (1) = 0,所以方程(*)的解为x 2 = 1,从而解得
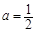 …………10分
…………10分另解:
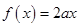 即
即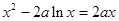 有唯一解,所以:
有唯一解,所以: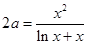 ,令
,令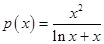 ,则
,则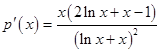 ,设
,设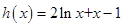 ,显然
,显然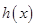 是增函数且
是增函数且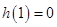 ,所以当
,所以当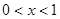 时
时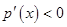 ,当
,当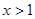 时
时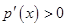 ,于是
,于是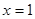 时
时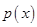 有唯一的最小值,所以
有唯一的最小值,所以 ,综上:
,综上: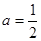 .
.(3)当
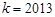 时, 问题等价于证明
时, 问题等价于证明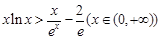
由导数可求
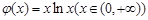 的最小值是
的最小值是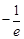 ,当且仅当
,当且仅当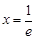 时取到,
时取到, 设
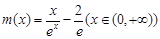 ,则
,则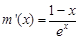 ,
,易得
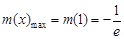 ,当且仅当
,当且仅当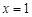 时取到,
时取到, 从而对一切
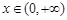 ,都有
,都有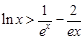 成立.故命题成立.…………16分
成立.故命题成立.…………16分点评:难题,利用导数研究函数的单调性、极值、最值,不等式恒成立问题,是导数应用的常见问题,本题因为参数的引入,增大了讨论的难度,学生易出错。不等式恒成立问题,往往通过构造函数,研究函数的最值,使问题得解。

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
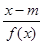 >
>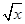 成立,求实数m的取值范围;
成立,求实数m的取值范围; 与
与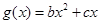 的图像都过点
的图像都过点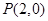 ,且它们在点
,且它们在点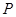 处有公共切线.
处有公共切线.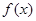 和
和 的表达式及在点
的表达式及在点 ,其中
,其中 ,求
,求 的单调区间.
的单调区间.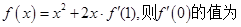 ____________。
____________。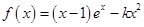 (其中
(其中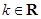 ).
).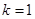 时,求函数
时,求函数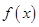 的单调区间;
的单调区间;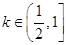 时,求函数
时,求函数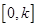 上的最大值
上的最大值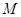 .
. 的图象在点
的图象在点 处的切线斜率为
处的切线斜率为 .
. 的值;
的值; 根的个数,证明你的结论;
根的个数,证明你的结论; ,使得曲线
,使得曲线 在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.
在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.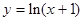
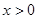 ,证明
,证明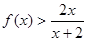 ;
;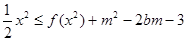 时
时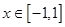 和
和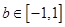 都恒成立,求实数
都恒成立,求实数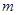 的取值范围。
的取值范围。 在其定义域内的一个子区间
在其定义域内的一个子区间 内有最小值,可求得实数
内有最小值,可求得实数 的取值范围是
的取值范围是 ,则
,则
 .
.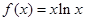
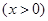 。
。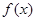 的最小值;
的最小值; 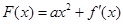
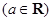 ,讨论函数
,讨论函数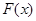 的单调性;
的单调性;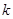 的直线与曲线
的直线与曲线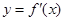 交于
交于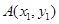 ,
,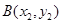
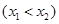 两点,求证:
两点,求证: 。
。