题目内容
15.在直三棱柱ABC-A1B1C1中,AB=BC=1,AC=$\sqrt{2}$,BB1=2,点M为BB1的中点,则点A到平面A1CM距离为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3\sqrt{2}}{2}$ |
分析 以B为原点,BA为x轴,BC为y轴,BB1为z轴,建立空间直角坐标系,利用向量法能求出点A到平面A1CM距离.
解答 解:∵直三棱柱ABC-A1B1C1中,AB=BC=1,AC=$\sqrt{2}$,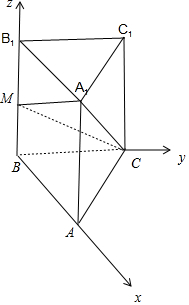
∴BC2+AB2=AC2,∴AB⊥BC,
以B为原点,BA为x轴,BC为y轴,BB1为z轴,建立空间直角坐标系,
∵BB1=2,∴A(1,0,0),A1(1,0,2),C(0,1,0),
M(0,0,1),
$\overrightarrow{M{A}_{1}}$=(1,0,1),$\overrightarrow{MC}$=(0,1,-1),$\overrightarrow{MA}$=(1,0,-1),
设平面A1CM的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{M{A}_{1}}=x+z=0}\\{\overrightarrow{n}•\overrightarrow{MC}=y-z=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,-1,-1),
∴点A到平面A1CM距离d=$\frac{|\overrightarrow{n}•\overrightarrow{MA}|}{|\overrightarrow{n}|}$=$\frac{2}{\sqrt{3}}$=$\frac{2\sqrt{3}}{3}$.
故选:B.
点评 本题考查点到平面的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
20.PA、PB、PC是从P点引出的三条射线,每两条的夹角为60°,则直线PC与平面APB所成角的余弦值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
5.质检过后,某校为了解理科班学生的数学、物理学习情况,利用随机数表法从全年级600名理科生抽取100名学生的成绩进行统计分析,已知学生考号的后三位分别为000,001,002,…,599.
(1)若从随机数表的第5行第7列的数开始向右读,请依次写出抽取的前7人的后三位考号;
(2)如果题(1)中随机抽取到的7名同学的数学、物理成绩(单位:分)对应如表:
从这7名同学中随机抽取3名同学,记这3名同学中数学和物理成绩均为优秀的人数为ζ,求ζ的分布列和数学期望(规定成绩不低于120分的为优秀).附:(下面是摘自随机数表的第4行到第6行)

(1)若从随机数表的第5行第7列的数开始向右读,请依次写出抽取的前7人的后三位考号;
(2)如果题(1)中随机抽取到的7名同学的数学、物理成绩(单位:分)对应如表:
| 数学成绩 | 90 | 97 | 105 | 113 | 127 | 130 | 135 |
| 物理成绩 | 105 | 116 | 120 | 127 | 135 | 130 | 140 |

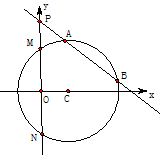 已知圆心在x轴正半轴上的圆C与直线5x+12y+21=0相切,与y轴交于M,N两点,且∠MCN=120°.
已知圆心在x轴正半轴上的圆C与直线5x+12y+21=0相切,与y轴交于M,N两点,且∠MCN=120°.