题目内容
10.在平面直角坐标系中,矩形ABCD的对角线所在的直线相较于(0,1),若边AB所在的直线的方程为x-2y-2=0,则圆(x-1)2+(y-1)2=9被直线CD所截的弦长为( )| A. | 3 | B. | $2\sqrt{3}$ | C. | 4 | D. | $3\sqrt{2}$ |
分析 求出直线x-2y-2=0上的点(2,0)关于点(0,1)的对称点,设出直线CD的方程,根据待定系数法求出直线CD的方程,求出圆心(1,1)到直线CD的距离,即可求出圆(x-1)2+(y-1)2=9被直线CD所截的弦长.
解答 解:直线x-2y-2=0上的点(2,0)关于点(0,1)对称点为(-2,2),
设直线CD的方程为x-2y+m=0,则直线CD过(-2,2),解得m=6,
所以边CD所在直线的方程为x-2y+6=0,
圆心(1,1)到直线CD的距离为$\frac{|1-2+6|}{\sqrt{1+4}}$=$\sqrt{5}$,
∴圆(x-1)2+(y-1)2=9被直线CD所截的弦长为2$\sqrt{9-5}$=4,
故选C.
点评 本题考查了求直线方程问题,考查直线的平行关系以及关于点对称问题,考查直线与圆的位置关系,考查弦长问题,是一道中档题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
20.PA、PB、PC是从P点引出的三条射线,每两条的夹角为60°,则直线PC与平面APB所成角的余弦值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
1.已知tanα=2,则sin2α+sinαcosα的值为( )
| A. | $\frac{6}{5}$ | B. | 1 | C. | $\frac{4}{5}$ | D. | $\frac{2}{3}$ |
5.质检过后,某校为了解理科班学生的数学、物理学习情况,利用随机数表法从全年级600名理科生抽取100名学生的成绩进行统计分析,已知学生考号的后三位分别为000,001,002,…,599.
(1)若从随机数表的第5行第7列的数开始向右读,请依次写出抽取的前7人的后三位考号;
(2)如果题(1)中随机抽取到的7名同学的数学、物理成绩(单位:分)对应如表:
从这7名同学中随机抽取3名同学,记这3名同学中数学和物理成绩均为优秀的人数为ζ,求ζ的分布列和数学期望(规定成绩不低于120分的为优秀).附:(下面是摘自随机数表的第4行到第6行)

(1)若从随机数表的第5行第7列的数开始向右读,请依次写出抽取的前7人的后三位考号;
(2)如果题(1)中随机抽取到的7名同学的数学、物理成绩(单位:分)对应如表:
| 数学成绩 | 90 | 97 | 105 | 113 | 127 | 130 | 135 |
| 物理成绩 | 105 | 116 | 120 | 127 | 135 | 130 | 140 |

2.设集合M={x|x2≤x},N={x|lgx≤0},则M∩N=( )
| A. | [0,1] | B. | (0,1] | C. | [0,1) | D. | (-∞,1] |
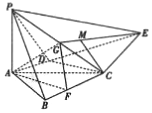 在四棱锥P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G为PC的中点,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分别为BC,EG上一点,且AF∥CD.
在四棱锥P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G为PC的中点,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分别为BC,EG上一点,且AF∥CD.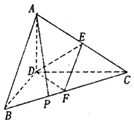 已知三棱锥A-BCD,AD⊥平面BCD,BD⊥CD,AD=BD=2,CD=2$\sqrt{3}$,E,F分别是AC,BC的中点.
已知三棱锥A-BCD,AD⊥平面BCD,BD⊥CD,AD=BD=2,CD=2$\sqrt{3}$,E,F分别是AC,BC的中点.