题目内容
5.若双曲线$\frac{{x}^{2}}{16+k}$-$\frac{{y}^{2}}{8-k}$=1(-16<k<8)的一条渐近线方程是y=-$\sqrt{3}$x,点P(3,y0)与点Q是双曲线上关于坐标原点对称的两点,则四边形F1QF2P的面积是.| A. | 12$\sqrt{6}$ | B. | 6$\sqrt{6}$ | C. | 12$\sqrt{2}$ | D. | 6$\sqrt{2}$ |
分析 求出双曲线的渐近线方程,解方程可得k=-10,求出双曲线的a,b,c,代入点P,可得纵坐标,由题意可得四边形F1QF2P为平行四边形,求出三角形PF1F2的面积,即可得到所求面积.
解答 解:双曲线$\frac{{x}^{2}}{16+k}$-$\frac{{y}^{2}}{8-k}$=1(-16<k<8),
可得渐近线方程为y=±$\sqrt{\frac{8-k}{16+k}}$x,
由题意可得$\sqrt{\frac{8-k}{16+k}}$=$\sqrt{3}$,
解得k=-10,
即有双曲线的方程为$\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{18}$=1,
可得c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{6+18}$=2$\sqrt{6}$,
设P在第一象限,代入双曲线方程可得
y0=3$\sqrt{2}$×$\sqrt{\frac{9}{6}-1}$=3.
即有P(3,3),
由P,Q关于原点对称,
可得四边形F1QF2P为平行四边形,
三角形PF1F2的面积为$\frac{1}{2}$|F2F1|•y0=$\frac{1}{2}$×4$\sqrt{6}$×3=6$\sqrt{6}$,
即有四边形F1QF2P的面积是2×6$\sqrt{6}$=12$\sqrt{6}$.
故选:A.
点评 本题考查双曲线的方程和性质,主要是渐近线方程的运用,考查平行四边形面积的求法,注意运用三角形的面积求法,考查化简整理的运算能力,属于中档题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
16.已知倾斜角为α的直线l与直线x+2y-4=0垂直,则$cos(\frac{2017}{2}π-2α)$的值为( )
| A. | 2 | B. | $-\frac{1}{2}$ | C. | $\frac{4}{5}$ | D. | $-\frac{4}{5}$ |
20.PA、PB、PC是从P点引出的三条射线,每两条的夹角为60°,则直线PC与平面APB所成角的余弦值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |

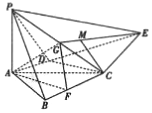 在四棱锥P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G为PC的中点,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分别为BC,EG上一点,且AF∥CD.
在四棱锥P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G为PC的中点,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分别为BC,EG上一点,且AF∥CD.