题目内容
7．在用线性回归方程研究四组数据的拟合效果中，分别作出下列四个关于四组数据的残差图，则用线性回归模式拟合效果最佳的是（ ）| A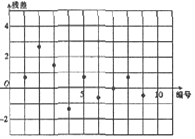． |  | B． |  | ||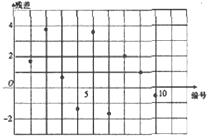
| C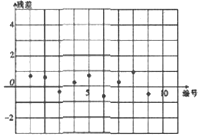． |  | D． |  |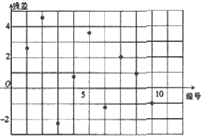
分析 根据残差点比较均匀地落在水平的袋装区域中，
且带状区域的宽度越窄，拟合精度越好，拟合效果越好，
由此得出结论．
解答 解：当残差点比较均匀地落在水平的袋装区域中，说明选用的模型比较合适，
这样的带状区域的宽度越窄，说明拟合精度越好，拟合效果越好，
对比4个残差图，易知选项C的图对应的袋装区域的宽度越窄．
故选：C．
点评 本题考查了残差图的应用问题，是基础题．
练习册系列答案
寒假大串联黄山书社系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
17．已知过原点的直线l1与直线l2：x+3y+1=0垂直，圆C的方程为x2+y2-2ax-2ay=1-2a2（a＞0），若直线l1与圆C交于M，N两点，则当△CMN的面积最大时，圆心C的坐标为（ ）
| A． | $（{\frac{{\sqrt{5}}}{2}，\frac{{\sqrt{5}}}{2}}）$ | B． | $（{\frac{{\sqrt{3}}}{2}，\frac{{\sqrt{3}}}{2}}）$ | C． | $（{\frac{1}{2}，\frac{1}{2}}）$ | D． | （1，1） |
2．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右顶点和上顶点分别为A，B，左焦点为F，以原点O为圆心的圆与直线BF相切，且该圆与y轴的正半轴交于点C，过点C的直线交椭圆于M，N两点，若四边形FAMN是平行四边形，则该椭圆的离心率为（ ）
| A． | $\frac{3}{5}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
19．函数f（x）=$\sqrt{x+1}$+lg（6-3x）的定义域为（ ）
| A． | （-∞，2） | B． | （2，+∞） | C． | [-1，2） | D． | [-1，2] |