题目内容
若a和b是计算机在区间（0，2）上产生的随机数，那么函数f（x）=lg（ax2+4x+4b）的值域为R（实数集）的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：几何概型
专题：概率与统计
分析：运用函数f（x）=lg（ax2+4x+4b）的值域为R（实数集），求出a，b的范围，再由几何概概型的概率公式，即可得到．
解答：
解：由已知，a和b是计算机在区间（0，2）上产生的随机数，对应区域的面积为4，
因为函数f（x）=lg（ax2+4x+4b）的值域为R（实数集），所以（ax2+4x+4b）能取得所有的正数，所以
，解得ab≤1且a＞0，对应的区域面积为
(2-
)da=（2a-lna）|
=3-2ln2；
由几何概型的公式得
；
故选B．
因为函数f（x）=lg（ax2+4x+4b）的值域为R（实数集），所以（ax2+4x+4b）能取得所有的正数，所以
|
| ∫ | 2
|
| 1 |
| a |
2
|
由几何概型的公式得
| 3-2ln2 |
| 4 |
故选B．
点评：本题考查的知识点是几何概型的意义，关键是要找出（0，2）上产生两个随机数a和b所对就图形的面积，几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．
练习册系列答案
相关题目
下列各组函数表示同一函数的是（ ）
A、y=
| |||
B、y=
| |||
| C、y=x+1，y=t-1 | |||
D、y=
|
已知点A（-2，0）和B（0，2）在直线y=kx+k-1的同侧，则实数k的取值范围是（ ）
| A、（-∞，-1）∪（3，+∞） |
| B、（-∞，-3）∪（1，+∞） |
| C、（-1，3） |
| D、（-3，1） |
将参加英语口语测试的1 000名学生编号为000，001，002，…，999，从中抽取一个容量为50的样本，按系统抽样的方法分为50组，如果第一组编号为000，001，002，…，019，且第一组随机抽取的编号为015，则抽取的第35个编号为（ ）
| A、700 | B、669 |
| C、676 | D、695 |
函数y=ln（
-1）的定义域为（ ）
| 1 |
| x |
| A、（0，1） |
| B、（1，+∞） |
| C、（-∞，0）∪（1，+∞） |
| D、（-∞，1） |
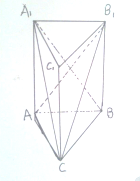如图，正三棱柱ABC-A1B1C1的边长及棱的长度均为2，求：