题目内容
定义
*
是向量
和
的“向量积”,它的长度|
*
|=|
||
|sinα,其中α为向量
和
的夹角,若
=(2,0),
-
=(1,-
),则|
*(
+
)|= .
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| u |
| u |
| v |
| 3 |
| u |
| u |
| v |
考点:平面向量数量积的含义与物理意义
专题:平面向量及应用
分析:由题意易得
和
+
的坐标,进而可得
•(
+
)和|
|以及|
+
|的值,可得cos<
,
+
>和sin<
,
+
>,由新定义代值可得.
| v |
| u |
| v |
| u |
| u |
| v |
| u |
| u |
| v |
| u |
| u |
| v |
| u |
| u |
| v |
解答:
解:∵
=(2,0),
-
=(1,-
),
∴
=(1,
),∴
+
=(3,
),
∴
•(
+
)=6
∴|
|=2,|
+
|=
=2
,
∴cos<
,
+
>=
=
,
∴sin<
,
+
>=
=
,
∴|
*(
+
)|=2×2
×
=2
故答案为:2
| u |
| u |
| v |
| 3 |
∴
| v |
| 3 |
| u |
| v |
| 3 |
∴
| u |
| u |
| v |
∴|
| u |
| u |
| v |
| 32+3 |
| 3 |
∴cos<
| u |
| u |
| v |
| 6 | ||
2×2
|
| ||
| 2 |
∴sin<
| u |
| u |
| v |
1-(
|
| 1 |
| 2 |
∴|
| u |
| u |
| v |
| 3 |
| 1 |
| 2 |
| 3 |
故答案为:2
| 3 |
点评:本题考查新定义,涉及向量的数量积和夹角公式,属基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
命题“函数y=f(x)的导函数为f′(x)=ex+
-
(其中e为自然对数的底数,k为实数),且f(x)在R上不是单调函数”是真命题,则实数k的取值范围是( )
| k2 |
| ex |
| 1 |
| k |
A、(-∞,-
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(
|
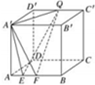 如图,正方体ABCD-A′B′C′D′的棱长为4,动点E,F在棱AB上,且EF=2,动点Q在棱D′C′上,则三棱锥A′-EFQ的体积( )
如图,正方体ABCD-A′B′C′D′的棱长为4,动点E,F在棱AB上,且EF=2,动点Q在棱D′C′上,则三棱锥A′-EFQ的体积( )| A、与点E,F位置有关 |
| B、与点Q位置有关 |
| C、与点E,F,Q位置有关 |
| D、与点E,F,Q位置均无关,是定值 |