题目内容
16.已知$\frac{{\sqrt{2}}}{2}({sin\frac{α}{2}-cos\frac{α}{2}})=\frac{{\sqrt{6}}}{3}$,则sinα的值为( )| A. | $-\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $-\frac{{2\sqrt{2}}}{3}$ |
分析 采用两边平方,根据同角函数关系式和二倍角的公式可得答案.
解答 解:由$\frac{{\sqrt{2}}}{2}({sin\frac{α}{2}-cos\frac{α}{2}})=\frac{{\sqrt{6}}}{3}$,
可得:$\frac{1}{2}$(sin2$\frac{α}{2}$+cos2$\frac{α}{2}$-2sin$\frac{α}{2}$cos$\frac{α}{2}$)=$\frac{2}{3}$
即1-sinα=$\frac{4}{3}$,
∴sinα=$-\frac{1}{3}$.
故选:A.
点评 本题主要考察了同角三角函数关系式和二倍角的公式的应用,属于基本知识的考查.

练习册系列答案
相关题目
6.已知某几何体的三视图如图,则该几何体的体积是( )
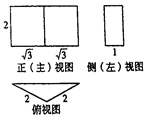

| A. | $\frac{{4\sqrt{3}}}{3}$ | B. | $4\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
4.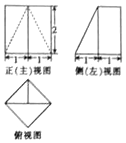 已知一个几何体的三视图如图所示,则该几何体的体积为( )
已知一个几何体的三视图如图所示,则该几何体的体积为( )
 已知一个几何体的三视图如图所示,则该几何体的体积为( )
已知一个几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{32}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
6.△ABC的内角A,B,C的对边分别为a,b,c,若$A=45°,a=\sqrt{2},b=\sqrt{3}$,则B等于( )
| A. | 30° | B. | 60° | C. | 30°或150° | D. | 60°或120° |